mojo's Blog
Scheduling with Deadlines with Disjoint Sets 본문
Kruskal’s Minimum Spanning Tree Algorithm
• Idea
– Finds an edge of the least possible weight that connects any two trees in the forest.
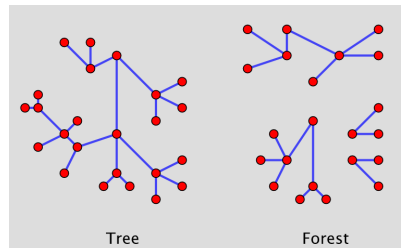
forest 내에서 두 개의 tree로 연결되어진 가중치가 최소가 되는 간선것을 찾는 아이디어를 활용한다.
즉, Disjoint-Set 을 이용하여 해결해야 한다.
• Implementation using disjoint-set data structure
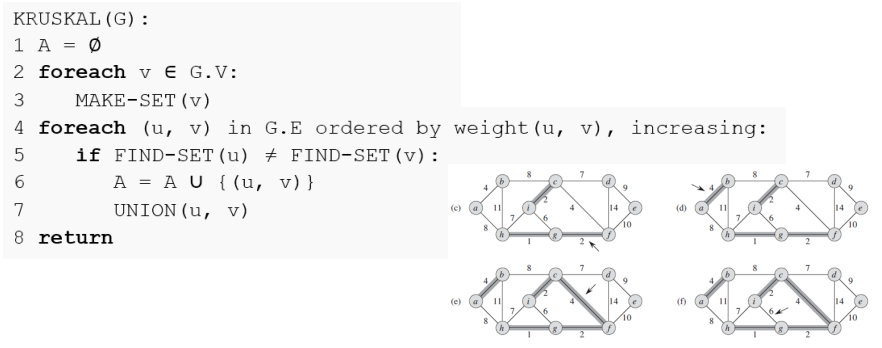
0. A 는 초기에 empty set으로 간선(u, v) 을 담기 위한 용도로 사용된다.
1. 먼저 MAKE-SET 함수를 통해 각 정점별로 자기 자신을 가르키도록 하도록(parent[v] = v) 설정한다.
2. 가중치가 적은 간선부터 시작하여 정점 u와 정점 v의 부모노드가 같지 않을 경우 A에 합치면서 동시에
u, v에 대한 Union 이 이뤄지도록 해야 한다.
3. A의 size가 (V - 1) 개가 된다면 MST 가 구현된 것이다.
• Complexity
– Sort the edges by weight: O(E log E)
– Process the edges until a tree is built: O(E log V)
➢ O(E log E + E log V) = O(E log V) why?
정점 V와 간선 E에 대해서 |V| = n, |E| = m 이라고 해보자.
Dense Graph 일 경우를 생각해본다면(worst case) m = O(n^2) 개의 간선이 존재하게 된다.
즉, O(E log E + E log V) = O(E log n^2 + E log n) = O(2E log n + E log n) = O(E log V) 이 된다.
(오더 관점에서 생각하기)
Scheduling with Deadlines with Disjoint Sets
• Problem
– Let J = {1, 2, …, n} be a set of jobs to be served.
– Each job takes one unit of time to finish.
– Each job has a deadline and a profit.
• If the job starts before or at its deadline, the profit is obtained.
➢ Schedule the jobs so as to maximize the total profit (not all jobs have to be scheduled).
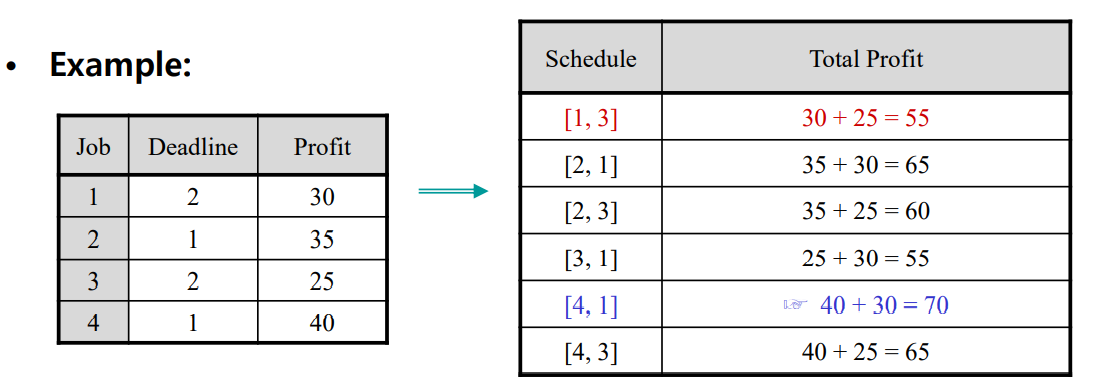
이전에 해당 문제를 구현한 방법은 링크드 리스트를 활용하여 O(n^2) 으로 해결하였다.
그러나 Disjoint-Sets 을 활용한다면 O(n log n) 의 효율을 뽑을 수 있다.
O(n log n) 으로 해결할 수 있는 방법을 살펴보도록 한다.
• Method
dmax : the maximum of the deadlines for n jobs.
Add a job as late as possible to the schedule being built, but no later than its deadline.
– Sort the jobs in non-increasing order by profit.
– Initialize dmax +1 disjoint sets, containing the integers 0, 1, 2, …, dmax.
– For each job in the sorted order,
• Find the set S containing the minimum of its deadline and n.
– If small(S) = 0, reject the job.
– Otherwise, schedule it at time small(S), and merge S with the set containing small(S)-1.
• Time complexity
– O(n log m) for the disjoint set manipulation, where m is the minimum of n and dmax.
– O(n log n) for sorting the profits
O(n log m)과 O(n log n)이 어디서 나온 시간복잡도인지를 확인해보려고 한다.
O(n log n) :
➢ 위에서 Sort the jobs in non-increasing order by profit 이라고 하였다.
즉, n개의 job의 profit 에 대해서 decreasing order 로 정렬하는 경우는 O(n log n) 이다.
O(n log m) :
➢ m = min(n, dmax) 임을 알아야 한다.
즉, 100개의 job에 대해서 deadline이 최대 10000이라고 가정한다면 100개를 채울 수 있고,
100개의 job에 대해서 deadline이 최대 10이라면 10개만에 채울 수 있다.
따라서 (m + 1)개에 대한 disjoint sets 을 초기화함으로써 union 하는 과정을 통해 O(n log m) 이 된다.
채우는 코드는 다음과 같다.
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
struct Job {
int job;
int Deadline;
int Profit;
};
struct subset {
int parent;
int rank;
int job;
int deadline;
int small;
};
void MakeSet(subset S[], int x) {
S[x].rank = 0;
S[x].parent = x;
S[x].small = x;
}
int max(int x, int y) {
return x > y ? x : y;
}
int min(int x, int y) {
return x < y ? x : y;
}
int Find(subset S[], int x) {
if (S[x].parent == x)
return x;
return (S[x].parent = Find(S, S[x].parent));
}
void Union(subset S[], int x, int y) {
x = Find(S, x), y = Find(S, y);
if (S[x].parent == S[y].parent)
return;
if (S[x].rank < S[y].rank) {
S[x].parent = y;
S[y].small = min(S[x].small, S[y].small);
}
else {
S[y].parent = x;
S[x].small = min(S[x].small, S[y].small);
if (S[x].rank == S[y].rank)
S[y].rank += 1;
}
}
Job job[100];
subset S[9];
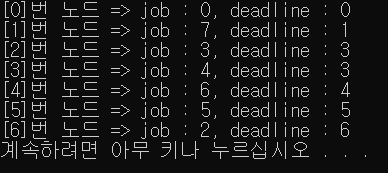
int deadline[12] = { 8,6,1,3,8,3,5,3,4,3,6,2 };
int profit[12] = { 90,45,55,85,10,65,75,60,40,20,30,95 };
int max_deadline = 8, job_cnt;
const int JOB = 12;
void PQ_insert(int n, int d, int p)
{
int x;
x = ++job_cnt;
while ((x != 1) && (job[x / 2].Profit < p)) {
job[x] = job[x / 2];
x /= 2;
}
job[x].job = n, job[x].Deadline = d, job[x].Profit = p;
}
Job PQ_pop()
{
int parent, child;
Job item, temp;
item = job[1], temp = job[job_cnt--];
parent = 1, child = 2;
while (child <= job_cnt) {
if ((child < job_cnt) && (job[child].Profit < job[child + 1].Profit)) child++;
if (temp.Profit >= job[child].Profit) break;
job[parent] = job[child];
parent = child;
child *= 2;
}
job[parent] = temp;
return item;
}
void Scheduling()
{
int i, d_max, x;
Job job;
d_max = 0;
for (i = 0; i < JOB; i++) {
d_max = max(d_max, deadline[i]);
PQ_insert(i + 1, deadline[i], profit[i]);
}
d_max = min(d_max, JOB);
// 0은 더미노드
for (i = 0; i <= d_max; i++)
MakeSet(S, i);
for (i = 0; i < JOB; i++) {
job = PQ_pop();
x = Find(S, job.Deadline);
if (S[x].small == 0)
continue;
S[x].job = job.job, S[x].deadline = job.Deadline;
Union(S, x - 1, job.Deadline);
}
for (i = 0; i <= d_max; i++) {
printf("[%d]번 노드 => job : %d, deadline : %d\n", i, S[i].job, S[i].deadline);
}
}
int main()
{
Scheduling();
return 0;
}
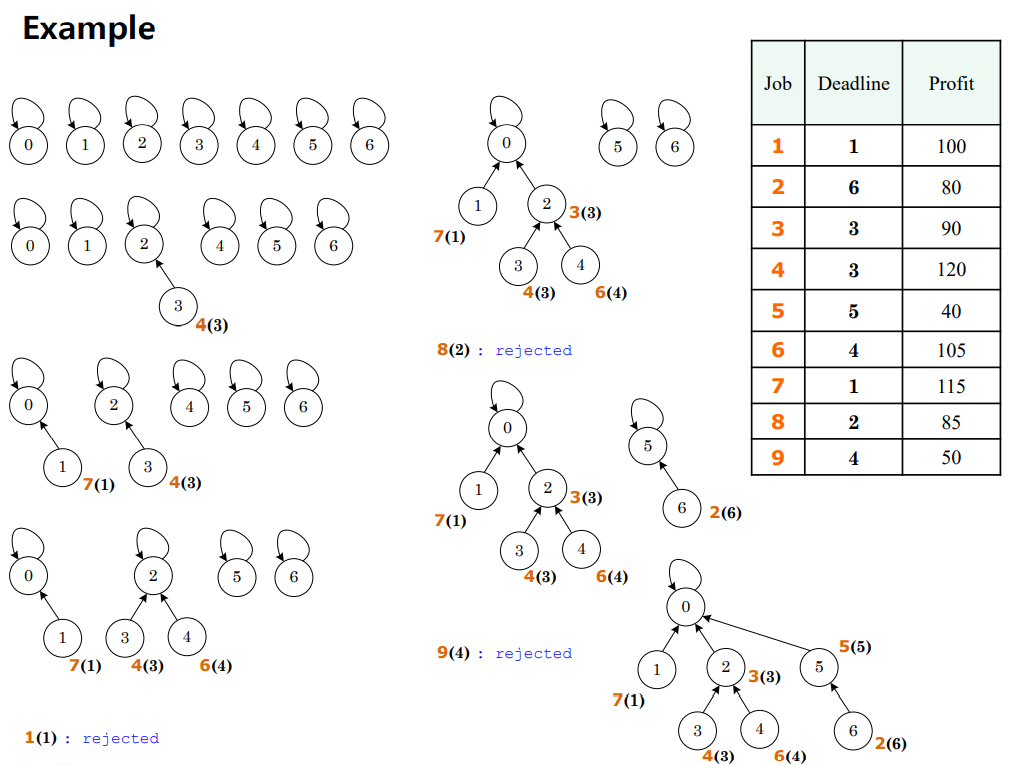
• Adjacency and incidence
– Two vertices v and w of a graph G are said to be adjacent if there is an edge joining them.
– Two distinct edges of G are adjacent if they have at least one vertex in common.
– The vertices v and w are then said to be incident to such an edge.
– The degree of a vertex v of G is the number of edges incident to v.
– A tree is a connected graph with no cycles.
– A forest is a graph with no cycles.
• Graph isomorphism
– Two graphs G1 and G2 are isomorphic if there is a one-to-one correspondence between the vertices
of G1 and those of G2 with the property that the number of edges joining any two vertices of G1 is
equal to the number of edges joining the corresponding vertices of G2
쉽게 말해서 그래프 G1, G2의 모양이 달라고 구조가 동일한 것을 의미한다.
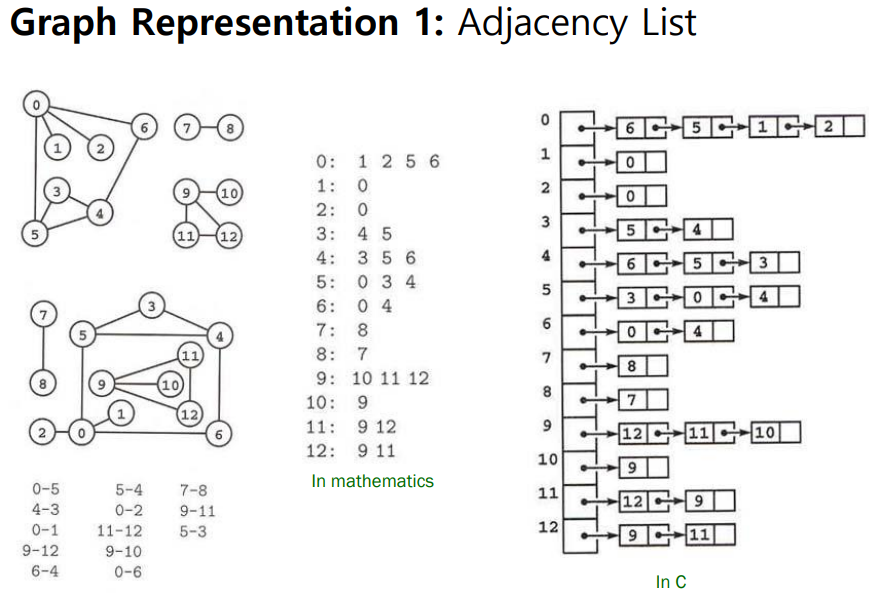
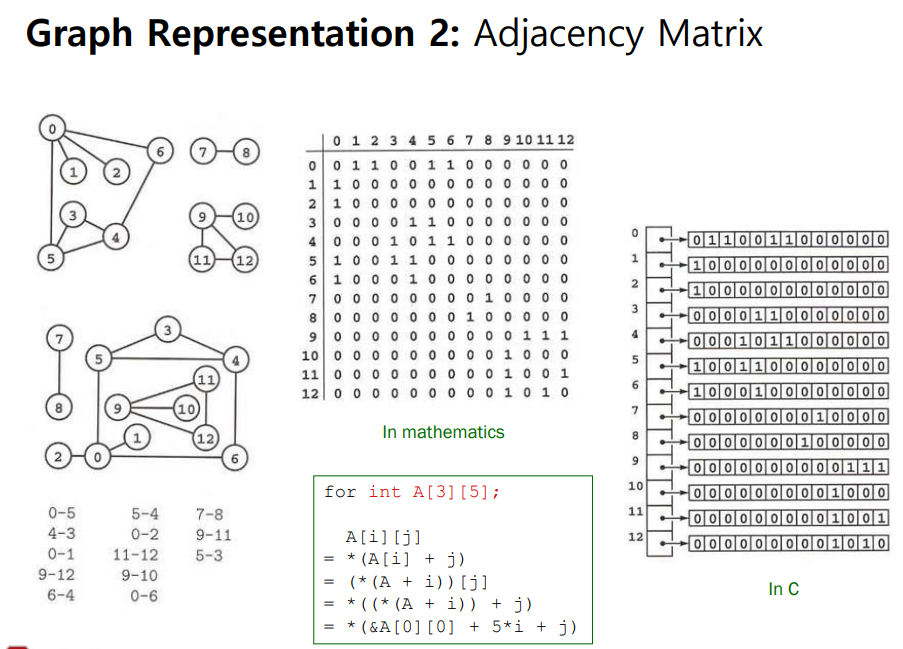
Adjacency List는 space complexity 가 적은 대신에 인접한 노드를 탐색하는데 드는 비용이 크고
Adjacency Matrix는 space complexity 가 큰 대신에 인접한 노드를 탐색하는데 드는 비용이 적다.
'학교에서 들은거 정리 > 알고리즘설계와분석' 카테고리의 다른 글
| Prim's Algorithm, Dijkstra's Algorithm (0) | 2021.12.09 |
|---|---|
| 인접 행렬을 이용한 다익스트라 구현 (0) | 2021.12.07 |
| Disjoint Sets (0) | 2021.11.30 |
| Scheduling with Deadlines (0) | 2021.11.25 |
| Scheduling (0) | 2021.11.23 |




