mojo's Blog
Scheduling 본문
Maximum Non-overlapping Intervals
이전에 Earliest finish first 방법이 가장 그럴듯 해 보인 방법임을 확인하였다.
따라서 이에 대한 알고리즘을 알아보도록 한다.
Greedy algorithm
Input : A = {a1, a2, ..., an} with ai = [si, fi] for 0 ≤ si < fi < ∞ (si : 시작 시간, fi : 끝나는 시간)
1. f1 ≤ f2 ≤ ... ≤ fn 순으로 정렬한다.
2. S = {a1}, k = 1, a1을 담아주고 담아준 인덱스를 k에 넣어준다.
3. j = 2부터 n까지 loop를 돌면서 sj ≥ fk 일 경우
=> S = S ∪ {aj}, k = j, aj를 담아주고 담아준 인덱스 j를 k에 넣어준다. (j = n 까지 반복)
4. S를 반환한다.
시간 복잡도는 1에서 O(nlogn), 3에서 O(n), 따라서 O(nlogn + n) = O(nlogn) 이다.
Scheduling: Minimizing Total Time in the System
Problem
– Consider a system in which a server is about to serve n clients.
Let T = {t1 , t2 , …, tn } be a set of positive numbers, where t i is the estimated time-to-completion
for the ith client.
What is the optimal order of service where the total (wait+service) time in the system is minimized?
– Hair stylist with waiting clients, pending operations on a shared hard disk, etc.
예를 들어서 T = {t1, t2, t3} = {5, 10, 4} 가 있다고 해보자.

A naive approach
- 모든 경우에 대해서 total값을 내서 그 중에 optimal solution을 찾는 것이다. => O(n!)
A greedy approach
- 주어진 T를 오름차순으로 정렬하는 방법이다. => O(nlogn)
Correctness: 위와 같은 그리디 방법이 항상 optimal solution을 찾을까?
• Let S = [s1 , s2 , …, sn ] be an optimal schedule, and C(S) be the total time for S.
• C(S) = s1 + (s1 + s2) + ... + (s1 + s2 + ... + sn)
= n*s1 + (n-1)*s2 + ... + sn
= Sigma(i = 1 to n){ (n + 1 - i) * si } = (n + 1) * Sigma(i = 1 to n){ si }- Sigma(i = 1 to n){ i * si }
• If they are not scheduled in nondecreasing order, then, for at least one i (1 ≤ i ≤ n -1), si > si+1.
• Now consider the schedule S’ = [s1 , s2 , …, si+1, si , …, sn ] that is obtained by interchanging
si and si+1.
• Then, 𝐶(𝑆') − 𝐶(𝑆) = (𝑖 ∙ 𝑠𝑖+1 + (𝑖 + 1) ∙ 𝑠𝑖) − (𝑖 ∙ 𝑠𝑖 + (𝑖 + 1) ∙ 𝑠𝑖+1) = 𝑠𝑖 − 𝑠𝑖+1 > 0.
결국 위와 같은 귀류법(Proof by contradiction)으로 해결책을 찾았다.
Scheduling: Minimizing Lateness
Problem
– Let J = {1, 2, …, n} be a set of jobs to be served by a single processor.
– The ith job takes ti units of processing time, and is due at time di .
– When the ith job starts at time si , its lateness li = max{0, si + ti - di }.
– Goal: Find a schedule S so as to minimize the maximum lateness L = max{ li }.
예를 들어서 다음과 같은 job 6개가 존재한다고 할 때,
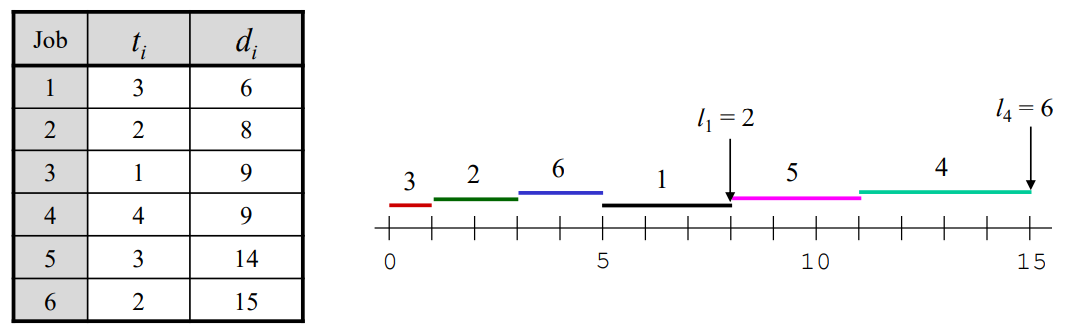
만약 S = {3, 2, 6, 1, 5, 4} 순으로 잡는다면 maximum lateness = 6 이다.
(임의로 잡은 것으로 Optimal solution이 아님)
즉, maximum lateness를 최소로 잡기 위해서 어떻게 해야 할까?
Earliest Deadline First 방법을 이용한다.
S = {1, 2, 3, 4, 5, 6} 순으로 잡는다면 maximum lateness = 1 이 된다.
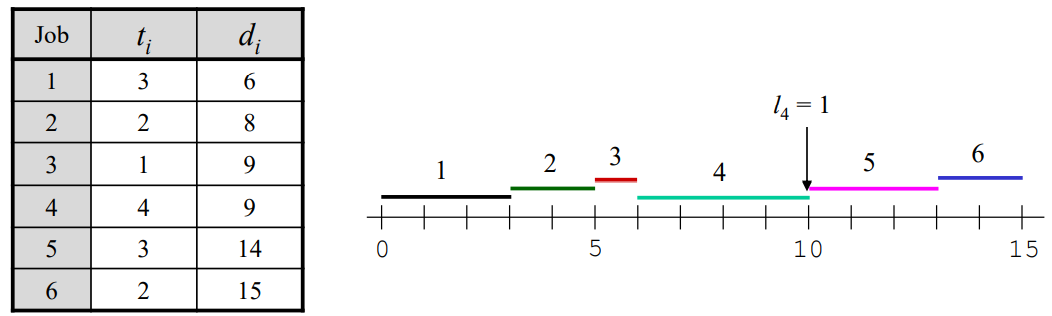
Correctness of "Earliest-deadline-first" - based algorithm
➢ 사실
1.만약 주어진 schedule에 inversion이 있을 경우, 최소한 연달아 schedule된 두 개의 inversion된 job이 있음.
• Inversion이란 deadline 관점에서 봤을 때 서로 순서가 뒤 바뀐 두 개의 job의 쌍 을 말함.
2.연달아 있는 inversion 상태의 두 개의 job의 순서를 서로 바꿀 경우, maximum lateness를 증가시키지 않음.
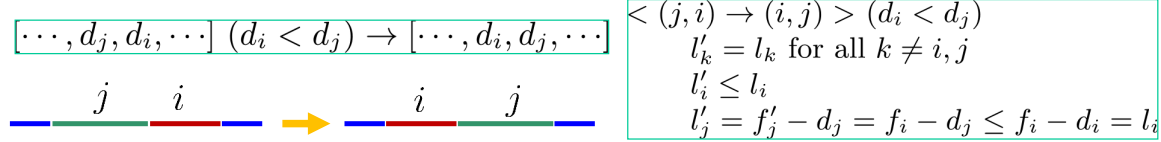
➢ 증명
1. S를 최소 개수의 inversion을 가지는 최적의 schedule이라 가정.
2.만약 S에 inversion이 없다면, 위의 방법으로 구한 schedule과 동일.
3.만약 S에 inversion이 있다면, 이 경우 연달아 있는 inversion된 두 job의 순서를 서로 바꾸면, 결과로 발생하는
schedule S’는 maximum lateness를 증가시키지 않음으로 역시 또 다른 최적의 schedule임.
4.그러나 S’는 S 보다 inversion의 개수가 적음. 이는 S에 대한 가정에 대한 모순.
따라서 S에는 inversion이 없고 따라서 이는 위의 방법으로 구한 schedule과 동일함.
'학교에서 들은거 정리 > 알고리즘설계와분석' 카테고리의 다른 글
| Scheduling with Deadlines with Disjoint Sets (0) | 2021.12.07 |
|---|---|
| Disjoint Sets (0) | 2021.11.30 |
| Scheduling with Deadlines (0) | 2021.11.25 |
| Huffman Coding (0) | 2021.11.16 |
| Subset Sum Problem (0) | 2021.11.09 |




