mojo's Blog
Bottom-up Parsing 본문
Bottom-up Parsing
Bottom-up parsing:
- Input string을 읽어가면서 reduce에 의해 start symbol을 찾아가는 방법
- Input string이 start symbol로 reduce되면 올바른 문장이라고 판단, 파스 트리 출력
- 그렇지 않으면 문법에 맞지 않은 문장으로 판단, 에러 메시지를 출력한다.
reduce, handle:
S ⇒* αAw ⇒ αβw의 유도 과정이 존재할 때
- reduce: sentential form αβw에서 β를 A로 대체하는 것
- handle: β. 즉 한 sentential form에서 reduce되는 부분.
ex ) rightmost derivation 과정을 보이고 parse tree를 그리고 handle 을 찾기
Sentence:
id + id ∗ id
① E → E + T
② E → T
③ T → T * F
④ T → F
⑤ F → (E)
⑥ F → id
1. rightmost derivation 과정을 보이자.
E => E + T (1)
=> E + T * F (3)
=> E + T * id (6)
=> E + F * id (4)
=> E + id * id (6)
=> T + id * id (2)
=> F + id * id (4)
=> id + id * id (6)
따라서 right parse : 6 4 2 6 4 6 3 1
2. parse tree 를 보이자.

3. handle 을 찾아보자.
| Sentential form | handle | production rule |
| id + id * id | id1 | F -> id (6) |
| F + id * id | F | T -> F (4) |
| T + id * id | T | E -> T (2) |
| E + id * id | id2 | F -> id (6) |
| E + F * id | F | T -> F (4) |
| E + T * id | id3 | F -> id (6) |
| E + T * F | T * F | T -> T * F (3) |
| E + T | E + T | E -> E + T (1) |
| E |
꿀팁 : production rule 부분에 right parse 를 차례로 작성한 다음에 구하자.
문법이 unambiguous하면 단 하나의 핸들만 존재한다: deterministic parsing 가능
handle pruning
S ⇒ ω1 ⇒ ω2 ⇒ ··· ⇒ ωn-1 ⇒ ωn = w의 rightmost derivation 과정이 있을 때,
- handle pruning: 각 ωi 의 sentential form에서 핸들을 찾아 ωi-1 로 reduce하면서
start symbol로 가는 과정
Shift-reduce parsing
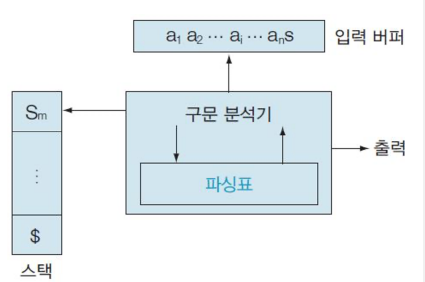
Shift-reduce Parser:
stack과 input buffer를 사용하여 구현
- Stack: handle을 찾기위한 grammar symbols을 유지. $로 초기화
- Input buffer: parsing될 input string을 유지. w$로 초기화
다음과 같은 행동을 갖는다:
- Shift: 현재의 input symbol을 스택의 top에 옮기는 것을 의미.
이 과정은 스택의 톱에 핸들이 나타날 때까지 계속
- Reduce: 핸들의 오른쪽 끝이 스택의 top에 나타나면 핸들의 왼 쪽 끝을 찾아서 완전한 형태의 핸들을 찾은 다음, rhs가 핸들인 production rule을 찾아 lhs에 있는 기호로 대체되는 것
- Accept: 주어진 string이 주어진 문법에 맞다는 것을 나타냄
- Error: 주어진 string이 주어진 문법에 맞지 않다는 것을 나타냄
① 초기 상태에서 시작하여 스택의 top에 핸들이 나타날 때까지 input symbol을 하나씩
stack으로 옮김 (shift).
② Shift를 하다가 핸들을 찾으면 production rule을 찾아 lfs에 있는 symbol로 reduce하고
부분 파스 트리를 구성한다.
③ 같은 방법으로 계속 진행한다. 핸들이 찾아지지 않거나 입력 버퍼가 비었는데 시작 기호가
나타나지 않으면 에러 출력.
④ 입력 문자열을 모두 읽은 후 start symbol을 만나면 accept.
ex ) Shift-reduce parsing 을 해보자.
Sentence: id + id ∗ id
① E → E + T
② E → T
③ T → T * F
④ T → F
⑤ F → (E)
⑥ F → id
| Step | Stack | Input symbol | Action |
| 1 | $ | id + id * id$ | shift id1 |
| 2 | $id1 | + id * id$ | Reduce F -> id |
| 3 | $F | + id * id$ | Reduce T -> F |
| 4 | $T | + id * id$ | Reduce E -> T |
| 5 | $E | + id * id$ | shift + |
| 6 | $E + | id * id$ | shift id2 |
| 7 | $E + id | * id$ | Reduce F -> id |
| 8 | $E + F | * id$ | Reduce T -> F |
| 9 | $E + T | * id$ | shift * |
| 10 | $E + T * | id$ | shift id |
| 11 | $E + T * id | $ | Reduce F -> id |
| 12 | $E + T * F | $ | T -> T * F |
| 13 | $E + T | $ | E -> E + T |
| 14 | $E | $ | Accept! |
ex ) Shift-reduce parsing 을 해보자 (위와는 약간 다른 Rule을 가진)
Sentence: id + id ∗ id
① E → E + E
② E → E ∗ E
③ E → id
④ E → (E)
먼저 rightmost derivation 을 구해보자.
E => E + E (1)
=> E + E * E (2)
=> E + E * id (3)
=> E + id * id (3)
=> id + id * id (3)
| Step | Stack | Input symbol | Action |
| 1 | $ | id + id * id$ | shift id |
| 2 | $id | + id * id$ | Reduce E -> id |
| 3 | $E | + id * id$ | shift + |
| 4 | $E + | id * id$ | shift id |
| 5 | $E + id | * id$ | Reduce E -> id |
| 6 | $E + E | * id$ | shift * |
| 7 | $E + E * | id$ | shift id |
| 8 | $E + E * id | $ | Reduce E -> id |
| 9 | $E + E * E | $ | Reduce E -> E * E |
| 10 | $E + E | $ | Reduce E -> E + E |
| 11 | $E | $ | Accept |
단계 5에서 id를 E로 reduce 하였지만, ∗ 를 shift 할 수도 있음
단계 6에서 ∗ 를 shift 했지만 E + E가 핸들이 될 수도 있음
즉, 문제가 있는 parsing 임을 알 수 있다.
Limitations:
- 핸들을 어떻게 찾을 것인가?
- 어떤 production rule을 적용할 것인가?
Solution:
- LR parsing
LR parser
LR(k) parser (Left-to-right and Right parse):
- L: input string을 왼쪽에서 오른쪽으로 읽어가며, R: right parse를 생성
- k: 한번에 읽는 input symbol의 개수. k=1일 경우 생략 가능
Strengths:
- Unambiguous CFG 로 쓰여진 모든 언어에 대해 구성 가능
- Deterministic parsing
- backtracking이 없음
- 에러 검출이 용이
Weakness:
- Top-down parser에 비해 구현이 복잡함
Parsing table in LR parser: action과 GOTO 로 구성
Variants: parsing table을 구성하는 방법에 따라서 분류
- SLR (simple LR): LR(0) item sets + FOLLOW 로 구성
- CLR (canonical LR): LR(1) item sets으로 구성
- LALR (lookahead LR): LR(0) item sets + lookahead 또는 LR(1) item sets으로 구성
LR(k) Grammar
- LR(k) grammar는 모든 entry에 대해 유일하게 정의되는 parsing table을 만들 수 있다.
Augmented Grammar
- Grammar G = (VN, VT, P, S)에 augment(첨가)된 문법
- G' = (VN∪{S'}, VT, P∪{S'→S}, S')로 표현됨
- S': start symbol
- S'→S : augmented production rule
Note:
production rule S'→S를 추가하는 이유
- Parser로 하여금 S를 S’로 reduce할 경우 이제 파싱을 끝내고 문장을 Accept 하도록 설계하기 위하여 사용
ex ) Augmented grammar를 만들어보기.
① E → E + E
② E → E * E
③ E → id
④ E → (E)
P :
E -> E + E | E * E | id | (E)
에서 S' -> E 를 추가해주자.
P' :
S' -> E
E -> E + E | E * E | id | (E)
따라서 G = ({S', E}, {+, *, id, (, )}, P', S') 이다.
LR(0) items
LR(0) item - rhs에 dot symbol를 가진 production rule이다
Production rule A → BCD의 LR(0) items:
[A → •BCD], [A → B•CD], [A → BC•D], [A → BCD•]
- A → B•CD: B를 읽었고 CD는 앞으로 읽을 기호임을 나타낸다.
- A → BCD•: BCD를 읽었고 이제 BCD를 A로 reduce할 수 있음을 의미한다.
Marking:
LR(0) item을 얻기 위해 production rule에 dot symbol을 추가하는 것
Mark symbol:
LR(0) item에서 dot symbol 오른쪽에 있는 기호
Three types of LR(0) items - Kernel item:
[A → α•β]에서 α ≠ ε이거나 A = S′인 경우
- Closure item: dot symbol이 rhs 맨 왼쪽에 있는 경우 (e.g., [A →•α])
- Reduce item: dot symbol이 rhs 맨 오른쪽에 있는 경우 (e.g., [A → α•])
Canonical collection (중요):
- 어떤 문법의 LR(0) items로 구성된 set
- LR parse table을 구성하는데 반드시 필요
CLOSURE(I)
CLOSURE(I), I는 문법 G에 대한 LR(0) item set.
CLOSURE(I)는 다음 규칙으로 구한다:
- 먼저 I에 속한 모든 LR(0) items를 CLOSURE(I)에 추가한다.
- CLOSURE(I) = I ∪ {[B → •γ] | [A → α•Bβ] ∈ CLOSURE(I), B→γ ∈P}
(1) [A → α•Bβ] ∈ CLOSURE(I)이고 B → γ가 존재하는 경우에, B →•γ가 CLOSURE(I)에 포함되어
있지 않으면 이 item을 CLOSURE(I)에 추가한다.
(2) 이 규칙은 새로운 LR(0) item이 CLOSURE(I)에 더 이상 추가될 수 없을 때까지 반복적으로
계속 적용된다.
CLOSURE(I) Algorithm
[입력] 문법 G, LR(0) item sets I
[출력] CLOSURE(I)
[방법]
begin
CLOSURE(I) = I;
repeat
if [A → α•Bβ]∈ CLOSURE(I) and B→γ ∈P
then CLOSURE(I) = CLOSURE(I) ∪[B → •γ]
until CLOSURE가 변하지 않을 때까지
end
ex ) LR(0) item E′ → •E와 E → E +•T의 CLOSURE를 구해보자.
Eʹ → E
E → E + T | T
T → T * F | F
F → (E) | id
CLOSURE([E′ → •E])
= {[E′ → •E], [E → •E + T], [E → •T], [T → •T * F], [T → •F], [F → •(E)], [F → •id]}
CLOSURE([E → E + •T])
= {[E → E + •T], [T → •T * F], [T → •F], [F → •(E)], [F → •id]}
GOTO function
LR(0) item의 GOTO Function
- Item set I와 X ∈ V에 대해, GOTO(I, X) = CLOSURE({[A → αX•β] | [A → α•Xβ] ∈ I}).
- Parsing을 위해서 mark symbol을 하나씩 읽는다는 의미
ex ) I = {[E′ → E•], [E → E•+ T]}일 때 GOTO(I, +)를 계산해보자.
P:
Eʹ → E
E → E + T | T
T → T * F | F
F → (E) | id
GOTO(I, +) = CLOSURE([E → E•+ T]) // 이때 {+} ∈ V 이며 [E → α•+β] ∈ I 를 만족하며
// [E′ → E•] 는 {+} 기호가 없으므로 만족하지 못함
CLOSURE([E → E + •T])
= {[E → E + •T], [T → •T * F], [T → •F], [F → •(E)], [F → •id]}
'학교에서 들은거 정리 > 기초컴파일러구성' 카테고리의 다른 글
| Semantic Analysis (0) | 2021.11.20 |
|---|---|
| LALR Parsing (0) | 2021.11.12 |
| CLR Parse / LALR Parse (0) | 2021.11.05 |
| SLR Parsing / CLR Parser (0) | 2021.11.04 |
| Canonical Collection (0) | 2021.10.30 |




