mojo's Blog
CLR Parse / LALR Parse 본문
Canonical Collection of LR(1) item sets
[알고리즘] Canonical Collection of LR(1) item sets
입력 : Augmented Grammar G'
출력 : Canonical Collection of LR(1) item sets
function CLOSURE(I);
begin
repeat
for each item [A → α•Bβ, a]∈I, each production rule B → 𝛄 ∈ G’
first(βa)에 포함되는 each terminal b에 대해서
do I = I U {[B → •𝛄, b]}
end for
until 더 이상 I에 새로운 item이 추가되지 않을 때
end
function GOTO(I, X);
begin
[A → α•Xβ, a]∈I 에 대해서 [A → αX•β, a] item set을 J라 하면
return CLOSURE(J)
end
Procedure items(G’);
begin
C = {CLOSURE({S’ → •S})};
repeat
for
Each I∈C, symbol X에 대해 GOTO(I,X)가 non-empty이고 C에 포함되지 않으면
do C = C U GOTO(I,X)
end for
until 더 이상 C에 새로운 item set I가 추가되지 않을 때
end
CLR Parse Table
[알고리즘] CLR 파싱표 구성
- [입력] G = (VN, VT , P, S)
- [출력] Augmented grammar G’에 대한 CLR parse table
- [방법]
1. G’에 대한 LR(1) item의 canonical collection C1 = {I0 , I1 , … In }을 구성한다.
2. State i는 I i에서 구성되고, state i를 위한 parsing action은 다음과 같다.
- 만약 LR(1) item [A → α•aβ, b]∈I i , GOTO(Ii , a) = Ij이면 action 표의 M[i, a] = Shift j
- 만약 LR(1) item [A → α•, a]∈I i 이면 action 표의 M[i, a] = Reduce A → α
- 만약 LR(1) item [S’ → S•, $]∈I i 이면 action 표의 M[i, $] = Accept
3. 만약 LR(1) item [A → α•Bβ, a]∈I i 이고 GOTO(Ii , B) = Ij 이면 GOTO 표의 M[i, B] = j
4. Augmented production rule의 LR(1) item [S’ → •S, $]를 포함하는 state는 initial state.
Example ) 다음 문법에서 LR(1) item의 Canonical collection을 구해보자.
S → CC
C → cC
C → d
1. Augmented grammar 을 추가한다.
S' → S
S → CC
C → cC
C → d
2. CLOSURE 를 구한다.
CLOSURE([S' → •S, $]) = {[S' → •S, $], [S → •CC, $], [C → •cC, c/d], [C → •d, c/d]} = I0
3. GOTO 를 구한다.
GOTO(I0, S) = CLOSURE([S' → S•, $])
= {[S' → S•, $]} = I1
GOTO(I0, C) = CLOSURE([S → C•C, $])
= {[S → C•C, $], [C → •cC, $], [C → •d, $]} = I2
GOTO(I0, c) = CLOSURE([C → c•C, c/d])
= {[C → c•C, c/d], [C → •cC, c/d], [C → •d, c/d]} = I3
GOTO(I0, d) = CLOSURE([C → d•, c/d])
= {[C → d•, c/d]} = I4
I1 는 GOTO 를 할 수 없다.
GOTO(I2, C) = CLOSURE([S → CC•, $])
= {[S → CC•, $]} = I5
GOTO(I2, c) = CLOSURE([C → c•C, $])
= {[C → c•C, $], [C → •cC, $], [C → •d, $]} = I6
GOTO(I2, d) = CLOSURE([C → d•, $])
= {[C → d•, $]} = I7
GOTO(I3, C) = CLOSURE([C → cC•, c/d])
= {[C → cC•, c/d]} = I8
GOTO(I3, c) = CLOSURE([C → c•C, c/d])
= {[C → c•C, c/d], [C → •cC, c/d], [C → •d, c/d]} = I3
GOTO(I3, d) = CLOSURE([C → d•, c/d])
= {[C → d•, c/d]} = I4
I4 는 GOTO 를 할 수 없다.
I5 는 GOTO 를 할 수 없다.
GOTO(I6, C) = {[C → cC•, $]} = I9
GOTO(I6, c) = {[C → c•C, $], [C → •cC, $], [C → •d, $]} = I6
GOTO(I6, d) = {[C → d•, $]} = I7
I7 는 GOTO 를 할 수 없다.
I8 는 GOTO 를 할 수 없다.
I9 는 GOTO 를 할 수 없다.
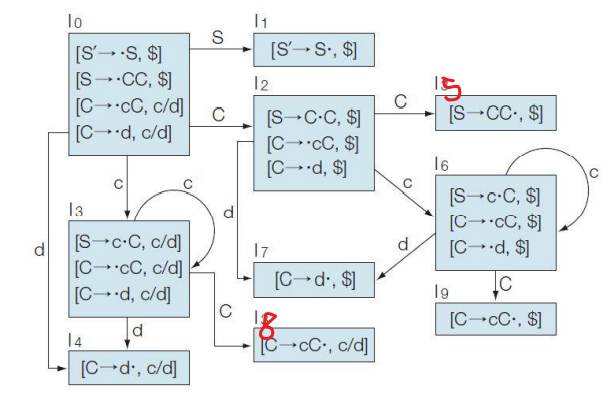
앞서 만든 Canonical collection 을 활용하여 CLR parsing table 을 구성해보자.
| State | Action | GOTO | |||
| c | d | $ | S | C | |
| 0 | s3 | s4 | 1 | 2 | |
| 1 | accept | ||||
| 2 | s6 | s7 | 5 | ||
| 3 | s3 | s4 | 8 | ||
| 4 | r3 | r3 | |||
| 5 | r1 | ||||
| 6 | s6 | s7 | 9 | ||
| 7 | r3 | ||||
| 8 | r2 | r2 | |||
| 9 | r2 | ||||
parsing table 을 활용하여 Sentence = "ccdd" 를 parsing 해보자
| Step | Stack | Input buffer | parsing |
| 0 | 0 | ccdd$ | s3 |
| 1 | 0c3 | cdd$ | s3 |
| 2 | 0c3c3 | dd$ | s4 |
| 3 | 0c3c3d4 | d$ | r3 |
| 4 | 0c3c3C | d$ | GOTO(3, C) = 8 |
| 5 | 0c3c3C8 | d$ | r2 |
| 6 | 0c3C | d$ | GOTO(3, C) = 8 |
| 7 | 0c3C8 | d$ | r2 |
| 8 | 0C | d$ | GOTO(0, C) = 2 |
| 9 | 0C2 | d$ | s7 |
| 10 | 0C2d7 | $ | r3 |
| 11 | 0C2C | $ | GOTO(2, C) = 5 |
| 12 | 0C2C5 | $ | r1 |
| 13 | 0S | $ | GOTO(0, S) = 1 |
| 14 | 0S1 | $ | accept! |
Example ) 다음 문법에서 LR(1) item의 Canonical collection 을 구해보자.
① S → L = R
② S → R
③ L → *R
④ L → id
⑤ R → L
(1) Augmented Grammar 을 추가하자
S' → S
S → L = R
S → R
L → *R
L → id
R → L
(2) CLOSURE 를 구하자
CLOSURE([S' → •S, $]) = {[S' → •S, $], [S → •L = R, $], [S → •R, $],
[L → •* R, = / $], [L → •id, = / $], [R → •L, $]} = I0
(3) GOTO 를 구하자 (생략)
...
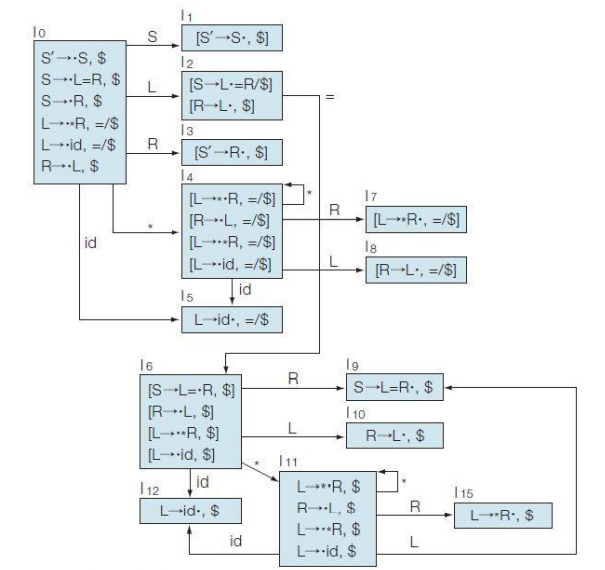
LALR Parser
CLR parsing
- SLR 방법보다 강력하다는 장점
- lookahead를 구하는 과정이 복잡하고 시간이 오래 걸리며 parse table이 크다는 단점
LALR parsing
- LR(1)과 같이 reduce action에서는 lookahead를 이용
- Parsing table의 크기를 되도록 작게 구성
Strengths
- SLR 방법보다 강력
- parse table의 크기가 CLR 방법보다 작음
- 프로그래밍 언어의 구문 구조를 대부분 편리하게 표현할 수 있음
(1) 모호하지 않은 문맥자유 문법으로 표현된 거의 모든 언어를 인식
(2) 에러를 초기에 탐지 가능
Weaknesses
- parse table을 만들기 위해 lookahead 기호를 구하는 것이 어려움
'학교에서 들은거 정리 > 기초컴파일러구성' 카테고리의 다른 글
| Semantic Analysis (0) | 2021.11.20 |
|---|---|
| LALR Parsing (0) | 2021.11.12 |
| SLR Parsing / CLR Parser (0) | 2021.11.04 |
| Canonical Collection (0) | 2021.10.30 |
| Bottom-up Parsing (0) | 2021.10.27 |




