mojo's Blog
LALR Parsing 본문
LALR Parser Implementation
1. 파싱표를 구성하기가 쉽지만 파싱표의 크기가 커지는 LR(1)을 가지고 구성
● 같은 코어를 가진 LR(1) item을 묶어서 하나의 state로 구성
2. 효율적으로 파싱표를 구성할 수 있는 LR(0)과 lookahead를 가지고 구성
● LR(1) item의 lookahead를 합한 것으로 구성
Example : LALR parse table을 구해보도록 하자.
P:
S -> CC
C -> cC
C -> d

I3, I6는 같은 코어이므로 lookahead 를 합친다.
I36 = {[S → c•C, c/d/$], [C → •cC, c/d/$], [C → •c, c/d/$]}
I4, I7는 같은 코어이므로 lookahead 를 합친다.
I47 = {[C → d•, c/d/$]}
따라서 LALR parse table을 만들면 다음과 같다.
| State | Action | GOTO | |||
| c | d | $ | S | C | |
| 0 | s36 | s47 | 1 | 2 | |
| 1 | accept | ||||
| 2 | s36 | s47 | 5 | ||
| 36 | s36 | s47 | |||
| 47 | r3 | r3 | r3 | ||
| 5 | r1 | ||||
| 89 | r2 | r2 | r2 | ||
LR(1) item set으로 부터 작성
● 이론적으로 쉽게 설명
● 하지만 C1 의 크기가 너무 커져서 비효율적
● Lookahead에 따라 state의 수가 매우 커지고 시간이 오래 걸리기 때문
LR(0) item set으로 부터 작성
● 이론적으로 복잡하고 어려움
● 하지만 시간적, 공간적으로 효율적임
LR(0) item set으로 부터 작성하는 방법
1. LR(0) item set의 canonical collection C0를 구성 (SLR과 동일)
2. Parse table의 shift, accept, GOTO action을 구성 (SLR과 동일)
3. Reduce action은 lookahead에 의해 결정 (LALR) 따라서, lookahead를 구하는 것이 핵심
PRED
[정의] State P의 previous state PRED(P)
p, q ∈C0 이고, X∈ V 이고, α, γ ∈V* 일 때,
GOTO(q, Xγ) = GOTO(GOTO(q, X), γ), where GOTO(q, ε) = q.
PRED(P, α) = {q | P ∈ GOTO(q, α)}.
Example : 다음 GOTO 그래프에서 I4의 previous state를 구해보자.
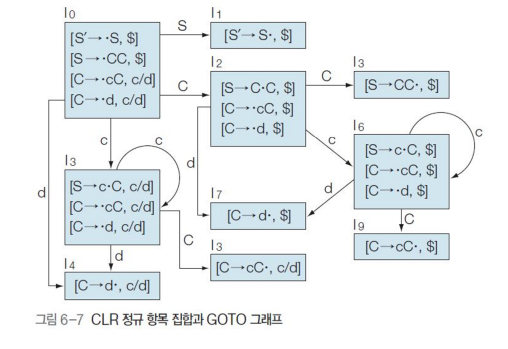
PRED(I4, d) = {I0, I3} 이다.GOTO(I0, d) = I4, GOTO(I3, d) = I4 이기 때문
Lookahead
[정의] lookahead
● State P에서 LR(0) item [A→α•β] 의 lookahead는 LA(P, [A→α•β])로 표기
● State P에서 nonterminal A 다음에 나올 수 있는 터미널 기호의 집합
LA(P, [A→α•β]) = {a | a ∈ FIRST(δ), S' ⇒* γAδ ⇒ γαβδ, γα accesses p} =
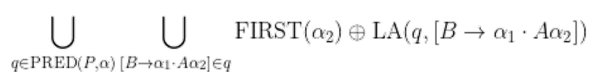
Note: γα accesses p: 시작 상태로부터 γα만큼 보고 state p로 이동을 하였다는 의미
Augmented grammar의 LR(0) item [S’ → •S], [S’ → S•]의 lookahead:
● LA(I0, [S’ → •S]) = LA(I1, [S’ → S•]) = {$}.
LALR parse table은 reduce에 대해서만 SLR과 다름
● lookahead 기호에 대해 파싱표를 만듬
● State P에서 reduce item [A → α•] 에 대해 다음과 같이 만든다:
for a ∈ LA(P, [A → α•]) do
M(P, a) = Reduce A → α
Example : Make LALR parsing table, and then parse the string *id = id.
0: S' → •S
1: S → L = R
2: S → R
3: L → *R
4: L → id
5: R → L
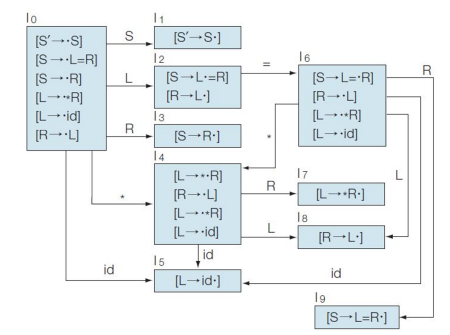
(1) LA(I0, [S' → •S]) = {$}
(2) LA(I1, [S' → S•]) = {$}
(3) LA(I2, [R → L•]) = FIRST(ε) ⊕ LA(I0, [S → •R])
= LA(I0, [S → •R])
= FIRST(ε) ⊕ LA(I0, [S' → •S])
= {$}
(4) LA(I3, [S → R•]) = FIRST(ε) ⊕ LA(I0, [S' → •S])
= {$}
(5) state I4는 Lookaside를 구할 수 없다.
(6) LA(I5, [L → id•]) 를 구하기 위해서 3가지 case로 나눠야 한다. (I0, I4, I6에서 오는 경우)
case I0 :
LA(I5, [L → id•]) = {FIRST(= R) ⊕ LA(I0, [S → •L = R])} ∪ {FIRST(ε) ⊕ LA(I0, [R → •L])}
= {=} ∪ LA(I0, [R → •L])
= {=} ∪ LA(I0, [S → •R])
= {=, $}
case I4:
LA(I5, [L → id•]) = FIRST(ε) ⊕ LA(I4, [R → •L])
= FIRST(ε) ⊕ LA(I4, [L → *•R])
= {FIRST(= R) ⊕ LA(I0, [S → •L = R])} ∪ LA(I0, [R → •L]) ∪ LA(I6, [R → •L])
= {=} ∪ {$} ∪ {FIRST(ε) ⊕ LA(I6, [S → L=•R])
= {=, $} ∪ {FIRST(ε) ⊕ LA[I0, S' → •S]}
= {=, $}
이 경우에는 추가로 I0, I6에서 오는 경우를 고려해줘야 한다. (주의하기)
case I6 :
LA(I5, [L → id•]) = FIRST(ε) ⊕ LA[I6, R → •L]
= FIRST(ε) ⊕ LA[I6, S → L=•R]
= FIRST(ε) ⊕ LA[I0, S' → •S]
= {$}
I0, I4, I6 case를 모두 고려한다면 최종적으로 LA(I5, [L → id•]) = {$, =} 이다.
(7) state I6은 Lookaside를 구할 수 없다.
(8) LA(I7, [L → *R•]) = {FIRST(=R) ⊕ LA(I0, [S → •L = R])} ∪ {FIRST(ε) ⊕ LA(I0, [R → •L])}
= {=, $}
(7) LA(I8, [R → L•]) 를 구하기 위해서 2가지 case로 나눠야 한다. (I4, I6에서 오는 경우)
case I4 :
LA(I8, [R → L•]) = FIRST(ε) ⊕ LA(I4, [L → *•R])
= {=, $}
case I6:
LA(I8, [R → L•]) = FIRST(ε) ⊕ LA(I6, [S → L =•R])
= {$}
I4, I6 case를 모두 고려한다면 최종적으로 LA(I8, [R → L•]) = {$, =} 이다.
(8) LA(I9, [S → L = R•]) = FIRST(ε) ⊕ LA(I0, [S' → •S])
= {$}
Lookahead을 모두 구했으므로 LALR Parsing 표를 구할 수 있다.
참고로 Lookahead가 없을 경우 next state로 이동하는 경우만 적고
있을 경우에 next state로 이동하는 경우 + reduce 둘 다 적어주면 적당한 표가 완성된다.
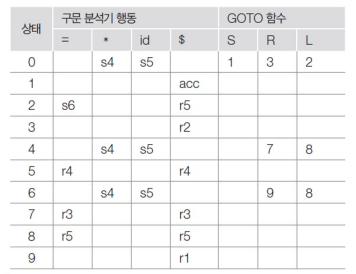
parsing 표를 확인하여 sentence = "*id = id" 를 인식해보자.
| Step | Stack | Input buffer | parsing |
| 0 | 0 | *id=id$ | s4 |
| 1 | 0*4 | id=id$ | s5 |
| 2 | 0*4id5 | =id$ | r4 |
| 3 | 0*4L | =id$ | GOTO(4, L) = 8 |
| 4 | 0*4L8 | =id$ | r5 |
| 5 | 0*4R | =id$ | GOTO(4, R) = 7 |
| 6 | 0*4R7 | =id$ | r3 |
| 7 | 0L | =id$ | GOTO(0, L) = 2 |
| 8 | 0L2 | =id$ | s6 |
| 9 | 0L2=6 | id$ | s5 |
| 10 | 0L2=6id5 | $ | r4 |
| 11 | 0L2=6L | $ | GOTO(6, L) = 8 |
| 12 | 0L2=6L8 | $ | r5 |
| 13 | 0L2=6R | $ | GOTO(6, R) = 9 |
| 14 | 0L2=6R9 | $ | r1 |
| 15 | 0S | $ | GOTO(0, S) = 1 |
| 16 | 0S1 | $ | Accept! |
이 문법은 LALR, CLR 문법이지만 SLR 문법은 아니다.
LALR 파싱표의 크기는 CLR 파싱표보다 작다.
Ambiguous Grammar
Ambiguous grammar:
● derivation 방식에 따라서 2개 이상의 파스 트리를 만들 수 있음
● 모든 ambiguous grammar는 LR grammar가 아님
Strengths:
● ambiguous grammar는 언어의 specification을 제공할 때 유용하다.
● 언어 구조에 대해 ambiguous grammar는 더 짧고 자연스러운 specification을 제공한다.
Weaknesses:
● Non-deterministic parsing
● Parse table을 작성할 때 항상 shift-reduce 충돌이나 reduce-reduce 충돌을 야기한다.
Handling Ambiguous Grammar
Handling ambiguous grammar:
1. Converting an ambiguous grammar to the equivalent unambiguous grammar
before making a parse table.
2. Or, make a parse table based on the ambiguous grammar, then remove conflict on the table.
2번째 방법을 이용하여 ambiguous grammar에 대한 parse table을 먼저 만들고
해당 테이블에 존재한는 conflict를 제거하는 방법으로 갈 것이다.
We will see how to use operator precedence and associativity rules to address conflicts.
● Production rule의 우선순위는 해당 rule에 포함된 terminal symbol로 결정
● Shift-reduce conflict
○ Production rule과 input symbol의 우선순위를 비교
■ Production rule의 우선순위가 높으면 reduce, 그렇지 않으면 shift.
○ 같은 우선순위일 때에는
■ Left associativity면 reduce, right associativity면 shift.
● Reduce-reduce conflict
○ Production rule들간의 우선순위를 비교
■ 높은 것을 선택하여 reduce.
○ 같은 우선순위일 때에는
■ Left associativity면 reduce, right associativity면 shift. (shift-reduce와 동일)
Example : 다음 문법에 대한 SLR parse table을 만들어보기
P:
E → E + E
E → E * E
E → (E)
E → id
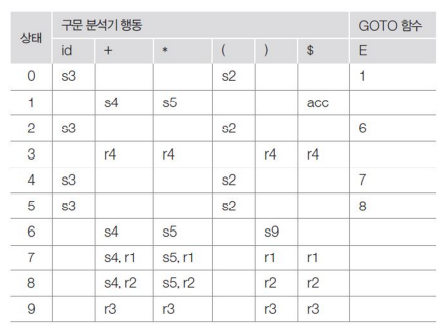
shift, reduce에 대한 충돌이 발생한 것으로 보인다.
이를 operator precedence와 associativty rule을 적용하여 충돌을 해결한다.
| State | Action | GOTO | |||||
| id | + | * | ( | ) | $ | E | |
| 0 | s3 | s2 | 1 | ||||
| 1 | s4 | s5 | Accept | ||||
| 2 | s3 | s2 | 6 | ||||
| 3 | r4 | r4 | r4 | r4 | |||
| 4 | s3 | s2 | 7 | ||||
| 5 | s3 | s2 | 8 | ||||
| 6 | s4 | s5 | s9 | ||||
| 7 | r1 | s5 | r1 | r1 | |||
| 8 | r2 | r2 | r2 | r2 | |||
| 9 | r3 | r3 | r3 | r3 | |||
I7 = {[E → E + E•], [E → E• + E], [E → E• * E]}
I8 = {[E → E * E•], [E → E• + E], [E → E• * E]}
I7 에서 '*' 에 대한 연산자는 reduce를 지우고 '+' 에 대한 연산자는 shift를 지운다.
I8 에서 '*' 에 대한 연산자는 shift를 지우고 '+' 에 대한 연산자는 reduce를 지운다.
이제 parse table로 sentence = "id + id * id" 에 대한 parsing을 해본다.
| Step | Stack | Input buffer | parsing |
| 0 | 0 | id+id*id$ | s3 |
| 1 | 0id3 | +id*id$ | r4 |
| 2 | 0E | +id*id$ | GOTO(0, E) = 1 |
| 3 | 0E1 | +id*id$ | s4 |
| 4 | 0E1+4 | id*id$ | s3 |
| 5 | 0E1+4id3 | *id$ | r4 |
| 6 | 0E1+4E | *id$ | GOTO(4, E) = 7 |
| 7 | 0E1+4E7 | *id$ | s5 |
| 8 | 0E1+4E7*5 | id$ | s3 |
| 9 | 0E1+4E7*5id3 | $ | r4 |
| 10 | 0E1+4E7*5E | $ | GOTO(5, E) = 8 |
| 11 | 0E1+4E7*5E8 | $ | r2 |
| 12 | 0E1+4E | $ | GOTO(4, E) = 7 |
| 13 | 0E1+4E7 | $ | r1 |
| 14 | 0E | $ | GOTO(0, E) = 1 |
| 15 | 0E1 | $ | Accept! |
Unambiguous grammar 에 대해서는 28단계의 과정을 거침
Ambiguous grammar + Operator precedence/associativity rule 은 16단계의 과정을 거침
따라서 Unambiguous grammar라고 하여도 conflict를 잘 해결할 수 있다면 더욱 효율적으로
parsing을 수행할 수 있다.
Example : 다음 문법에 대한 SLR parse table 만들어 보기
P:
S → iSeS
S → iS
S → a
augmented grammar를 추가하고 canonical collection을 구하면... 다음과 같다.
I0 = {[S' -> •S], [S -> •iSeS], [S -> •iS], [S -> •a]}
I1 = {[S' -> S•]}
I2 = {[S -> i•SeS], [S -> i•S], [S -> •iSeS], [S -> •iS], [S -> •a]}
I3 = {[S -> a•]}
I4 = {[S -> iS•eS], [S -> iS•]}
I5 = {[S -> iSe•S], [S -> •iSeS], [S -> •iS], [S -> •a]}
I6 = {[S -> iSeS•]}
Example : 충돌을 해결하고 sentence = "iiaea"의 파싱을 해보자. (else는 항상 가장 가까운 if에 걸림)
| State | Action | GOTO | |||
| i | e | a | $ | S | |
| 0 | s2 | s3 | 1 | ||
| 1 | accept | ||||
| 2 | s2 | s3 | 4 | ||
| 3 | r3 | r3 | |||
| 4 | s5(r2 제거) | r2 | |||
| 5 | s2 | s3 | 6 | ||
| 6 | r1 | r1 | |||
I4 = {[S -> iS•eS], [S -> iS•]} 에서 else는 항상 가장 가까운 if에 걸리도록 해야 하므로 reduce를 제거해준다.
| Step | Stack | Input buffer | parsing |
| 0 | 0 | iiaea$ | s2 |
| 1 | 0i2 | iaea$ | s2 |
| 2 | 0i2i2 | aea$ | s3 |
| 3 | 0i2i2a3 | ea$ | r3 |
| 4 | 0i2i2S | ea$ | GOTO(2, S) = 4 |
| 5 | 0i2i2S4 | ea$ | s5 |
| 6 | 0i2i2S4e5 | a$ | s3 |
| 7 | 0i2i2S4e5a3 | $ | r3 |
| 8 | 0i2i2S4e5S | $ | GOTO(5, S) = 6 |
| 9 | 0i2i2S4e5S6 | $ | r1 |
| 10 | 0i2S | $ | GOTO(2, S) = 4 |
| 11 | 0i2S4 | $ | r2 |
| 12 | 0S | $ | GOTO(0, S) = 1 |
| 13 | 0S1 | $ | Accept |
Error Processing Routine
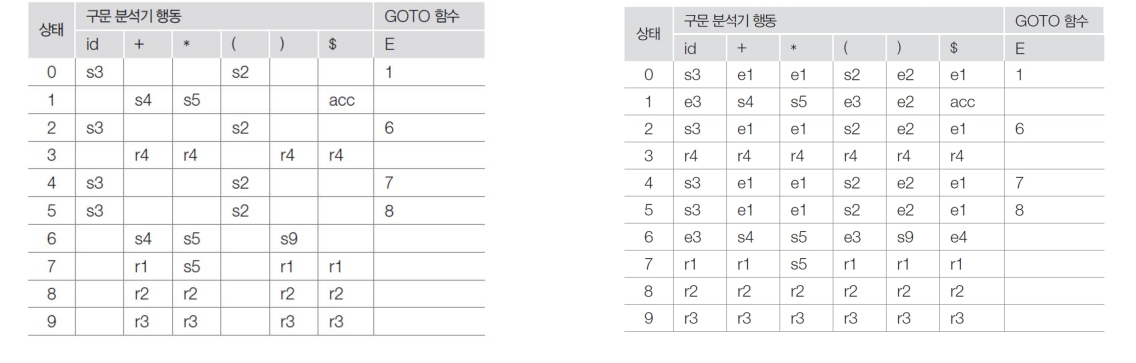
P:
E → E + E
E → E * E
E → (E)
E → id
위 Grammar에 대한 충돌을 제거한 파싱표와 에러 검출과 처리를 위한 파싱표 2개가 있다.
e1: State 0, 2, 4, 5로부터 호출된다.
이 states는 id를 기대하는데 +, *, $가 발견되었다. ‘missing operand’를 출력한다.
계속 처리한다면 id를 push 하고 state 3을 push 한다.
e2: 오른쪽 괄호를 발견했을 때 state 0, 1, 2, 4, 5로부터 호출된다.
왼쪽 괄호 없이 오른쪽 괄호를 발견한 경우이므로 입력에서 오른쪽 괄호를 제거하라고 하거나
왼쪽 괄호를 추가하라고 한다.
‘unbalanced right parenthesis’를 출력한다.
계속 처리한다면 입력에서 오른쪽 괄호를 제거 한다.
e3: 이 루틴은 state 1, 6으로부터 호출된다.
피연산자를 읽고 연산자를 기대하고 있는데 id나 왼쪽 괄호가 발견된 경우이다.
‘missing operator’를 출력한다.
계속 처리한다면 +를 push하고 state 4를 스택에 저장한다.
e4: 이 루틴은 state 6으로부터 호출된다.
오른쪽 괄호를 기대하는데 입력의 끝인 $가 발견되었다.
‘missing right parenthesis’를 출력한다.
계속 처리 한다면 오른쪽 괄호를 push하고 state 9를 스택에 저장한다
'학교에서 들은거 정리 > 기초컴파일러구성' 카테고리의 다른 글
| Intermediate Code Generation (0) | 2021.11.25 |
|---|---|
| Semantic Analysis (0) | 2021.11.20 |
| CLR Parse / LALR Parse (0) | 2021.11.05 |
| SLR Parsing / CLR Parser (0) | 2021.11.04 |
| Canonical Collection (0) | 2021.10.30 |




