mojo's Blog
Classification Problem 본문
※ Example: Linear Regression
Fitting a linear model with a set of variables \(x_{0}, x_{1}, ..., x_{d}\)
\(f(x) = w_{0}x_{0} + w_{1}x_{1} + ... + w_{d}x_{d} \)
Age and systolic blood pressure (SBP)
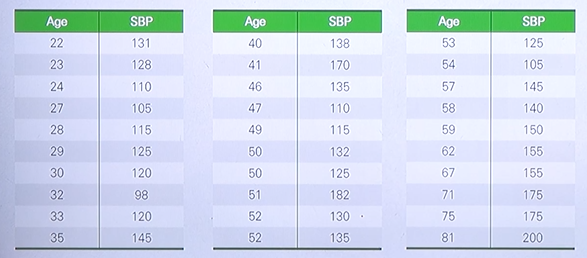
위 사진은 나이와 실제 blood pressure 혈압과의 관계를 표현한 데이터이다.
나이에 따라서 혈압이 오르는지 않오르는지 살펴보는 예제이다.
둘의 관계를 \(f(x)\) 와 같은 선형 함수로 표현이 된다고 가정한다.
이때, x는 age 밖에 존재하지 않으므로 \(f(x) = w_{1}x + w_{0}\) 의 모양으로 볼 수 있다.

normal equation 을 이용하여 위와 같이 혈압과 나이의 관계를 다음과 같은 선형함수로 표현할 수 있다.
\(SBP = 1.0538 \times Age + 87.361\)
※ Classification Problem
Age and coronary heart disease (CD)

How about applying the linear regression model for the classification problem?
이번엔 나이와 심장질환에 대한 관계이다.
이전과 다르게 이번엔 실수형 데이터가 아닌 정수형 데이터를 output 으로 다루고 있다.
regression 을 이용하여 문제를 해결할 수 있는지를 살펴보도록 한다.
In that case, the output can be > 1 or < 0.
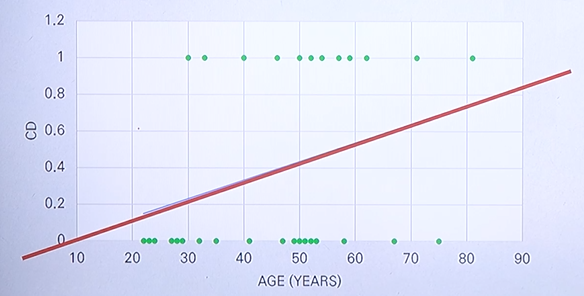
normal equation 을 이용하여 위와 같이 심장질환과 나이의 관계를 다음과 같은 선형함수로 표현할 수 있다.
\(CD = 0.0102 \times Age - 0.0755\)
위와 같이 표현이 되고 나이가 증가함에 따라 상대적으로 심장질환이 발생할 수 있는 확률이
높아진다는 것을 확인할 수 있다.
그러나 문제점으로 주어진 y에 대해 선형함수에 적용할 경우 0 또는 1의 값을 가져야 하는데
나이가 지나치게 작거나 큰 경우에는 1 이상의 값 또는 0 이하의 값을 가지는 경우가 발생하게 된다.
즉, 0 또는 1이 아닌 다른 값을 가질 수 있다는 것이 첫 번째 문제이다.
두 번째 문제는 주어진 데이터의 경우에 나이에 따라 심장질환이 일어난 경우에 관계가 있기 때문에
상대적으로 특정 값이 크게 벗어나는 경우가 없다.
그러나 나이가 어림에도 불구하고 심장질환이 있는 데이터가 존재할 경우 이 데이터에 따라서
주어진 선형 모델이 크게 변화할 수 있는 문제가 발생한다.
즉, 선형적으로 분류할 때 효과적이지 않은 데이터가 존재할 경우 학습하려는 선형 모델은
크게 바뀔 수 있다는 문제가 있다.
Simple Classification Model
※ Finding a Linear Decision Boundary

여기서 데이터는 \(x_{1}, x_{2}\) 2차원의 데이터로 표현되고 실제 \(y\) 에 해당되는 값은
위와 같이 색깔로 표현한 것이다.
y를 이진분류라고 가정할 경우, +인 부분을 파란색 엑스로 표현한 것이고 -인 부분을
빨간색 동그라미로 표현했다고 볼 수 있다.
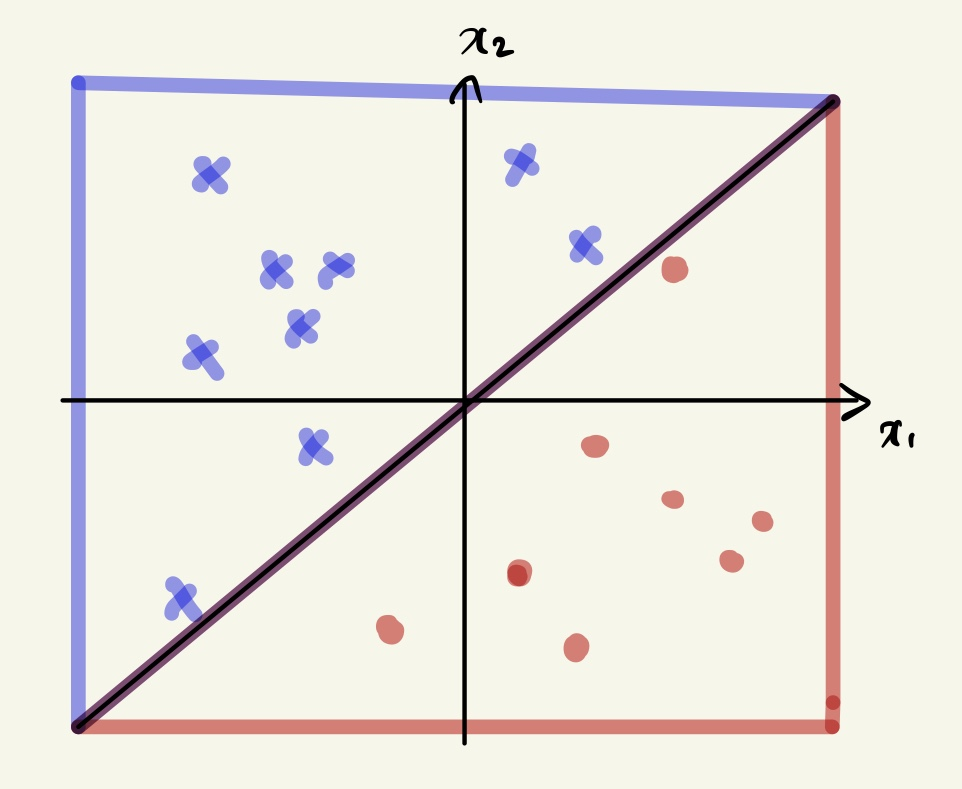
두 개의 서로 다른 레이블을 가진 데이터를 분류할 때 가장 많이 사용하는 방식은
위 데이터를 분류하는 임의의 어떤 decision boundary를 찾는 문제로 바라볼 수 있다.
데이터를 분류하기 위해 위와 같이 직선을 그어서 분류할 수 있다.
※ Review: Geometric Visualization
Calculating the angle between two vectors

\(cos(a) = \frac{w^{T}x}{\left\|w \right\| \left\|x \right\|} \Rightarrow cosa \propto w^{T}x\)
위 식과 같이 두 벡터의 내적과 그 벡터의 길이로 normalization한 식이 두 벡터의 각도라 볼 수 있다.
그리고 두 벡터의 내적에 비례한다고 볼 수 있다.
The angle is proportional to the dot product.
If \(w^{T}x > 0 \Rightarrow cosa > 0 \Rightarrow a < 90 \)
If \(w^{T}x < 0 \Rightarrow cosa < 0 \Rightarrow a > 90 \)
※ Geometric Visualization
Ideally, the weight vector should be like this:
- For positive samples, an angle is less than 90 degrees.
- For negative samples, an angle with more than 90 degrees.
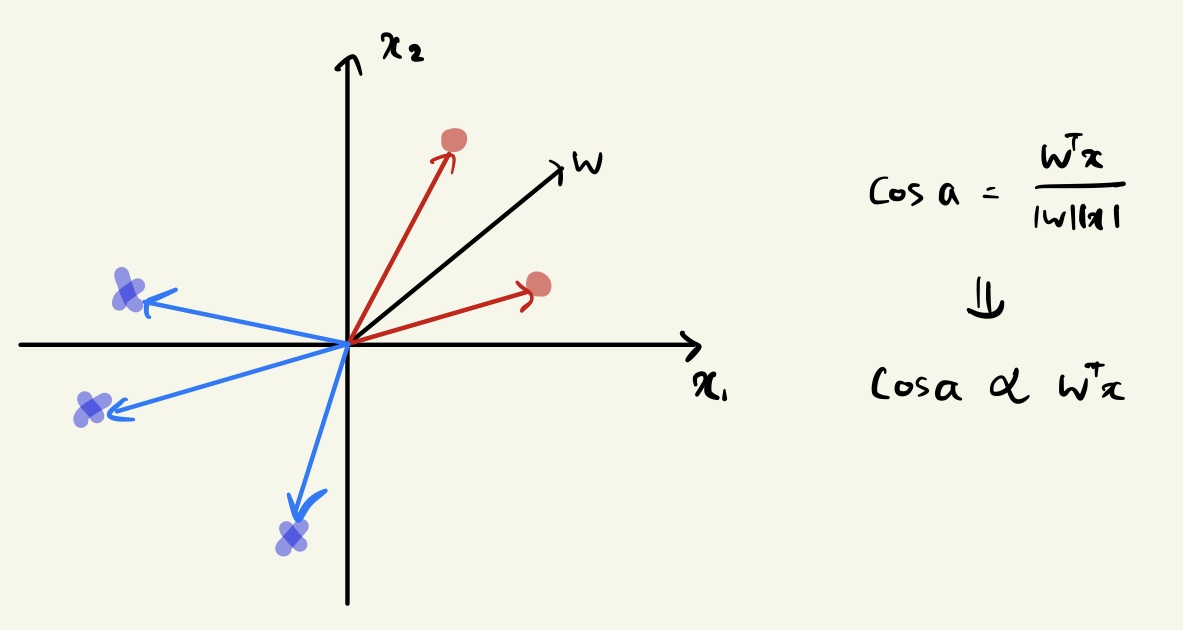
빨간색 점들은 w와의 각도가 90도보다 작은 것을 확인할 수 있다.
파란색 엑스들은 w와의 각도가 90도보다 큰 것을 확인할 수 있다.
즉, 주어진 데이터와 parameter인 w와의 각도를 통해서 각도가 양수이면 90도보다 작은 경우는
positive 샘플로 살펴볼 수 있고, 90도보다 큰 경우는 negative 샘플로 살펴볼 수 있다.
※ Case 1: How to Adjust an Angle
When x belong to the positive sample and \(w^{T}x < 0\),
We need to increase the \(cosa\) value.
-> we need to decrease the \(a\) value.

위와 같이 \(x\)가 positive 샘플임에도 불구하고 \(w\)와 \(x\)의 각도가 90도를 넘어서게 될 경우,
\(w_{new} = x + w\) 으로 새롭게 \(w\) 를 조정할 수 있다.
※ Case 2: How to Adjust an Angle
When x belong to the negative sample and \(w^{T}x > 0\),
We need to decreasing the \(cosa\) value.
-> we need to increase the \(a\) value.
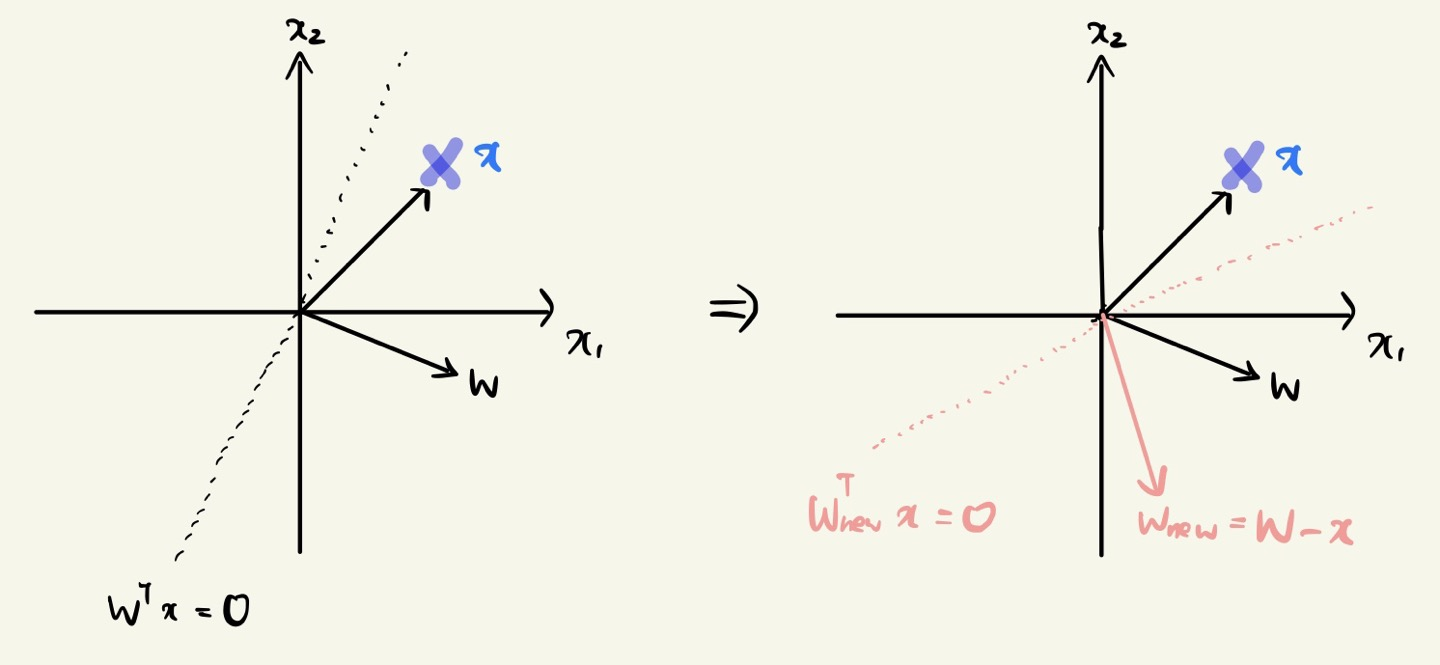
위와 같이 \(x\)가 negative 샘플임에도 불구하고 \(w\)와 \(x\)의 각도가 90도 미만일 경우,
\(w_{new} = w - x\) 으로 새롭게 \(w\) 를 조정할 수 있다.
※ Learning a Linear Classifier
Execute the algorithm until not encountering mistakes.
-> start from some \(w_{0}\) and 'correct' its makes on \(D\)
For \(t = 0, 1, ... \)
(1) find a mistake of \(w_{t}\) called \(\left ( x_{n(t)}, y_{n(t)} \right )\)
\(sign\left ( w_{t}^{T}x_{n(t)} \right ) \neq y_{n(t)}\)
(2) (try to) correct the mistake by
\(w_{t+1} \leftarrow w_{t}+y_{n(t)} x_{n(t)}\)
...until no more mistakes
return the last w
\(w_{t}\) 에 대해서 잘못 분류된 \(x_{n(t)}, y_{n(t)}\) 은 다음과 같은 경우이다.
\( sign\left ( w_{t}^{T}x_{n(t)} \right ) \neq y_{n(t)} \) 을 두 가지 경우로 본다면,
- \( w_{t}^{T}x_{n(t)} \) = +1, \(y_{n(t)}\) = -1 인 경우
- \( w_{t}^{T}x_{n(t)} \)= -1, \(y_{n(t)}\) = +1 인 경우
y가 positive 샘플인 경우 잘못 분류된 경우 \(w_{new} = w + x\) 으로 업데이트 해주고,
y가 negative 샘플인 경우 잘못 분류된 경우 \(w_{new} = w - x\) 으로 업데이트 해준다.
이러한 업데이트 과정을 계속하여 최종적으로 더 이상 실수가 일어나지 않을 때까지 계속해서 반복한다.
'머신러닝' 카테고리의 다른 글
| The Concept of Logistic Regression (0) | 2023.03.29 |
|---|---|
| Parameter Estimation (0) | 2023.03.21 |
| Linear Regression Models (0) | 2023.03.19 |
| Gradient Descent Method (0) | 2023.03.16 |
| Steps of Supervised Learning (0) | 2023.03.14 |




