mojo's Blog
Hard Disk Drives 본문
Hard Disk Drives
Hard drive 의 특성을 이해해야 내부적으로 어떻게 돌아가는지에 대해 알 수 있다!

Base Geometry

hard drive를 옆에서 본 측면이다.
platter가 3개 있고 platter 위아래 부분은 surface 이다. (density를 높이기 위해 아래에도 있음)
arm이 왔다 갔다하고 위아래에 존재함
예를 들어 foo파일이 첫번째 platter에 있다면 6개의 Disk head가 병렬적으로 센싱하지 않는다.
=> 하나만 active 상태가 되서 파일을 찾아감 (controller가 다 잡을 수 없기 때문 + 충분히 빠른 이유)

이번엔 위에서 본 hard drive 이다.
Arm이 왔다 갔다 하고 Sector가 512 byte로 존재한다.
읽거나 쓸 때 512 byte의 Sector단위로 읽고 쓴다.
A Simple Disk Drive

밖에 있는 것을 outer track, 안에 있는 걸 Inner track 이라함
0번부터 시작해서 시계방향으로 numbering 한다.
그 담에 11 => 12로 넘어가서 numbering 하고 23 => 24 로 넘어가서 numbering 하는 방식
총 36개의 Sector가 들어가므로 36 * 512 Byte = 18 KB 이다.
Rotation delay
만약 full rotation delay가 R일 경우, 30 -> 24 으로의 rotation delay는 당연하게도 R / 2 이다.
(반바퀴 돌았으므로)
Seek time

Inner most track 에서 Outer most track 으로 이동하는데 걸리는 시간을 Seek Time 이라고 한다.
Phase of seek
Acceleration -> Coasting -> Deceleration -> Setting time (about 0.5 ~ 2ms)
Acceleration, Coasting, Deceleration를 첫번째 phase로 보고
Setting time을 두번째 phase 라고 본다.
ex ) foo가 0번부터 있다고 가정해보자. (0 ~ 5)
1. head가 33번째에 있으면 먼저 outer 쪽으로 Seeking 하고

2. Rotation Delay가 걸림

Track skew
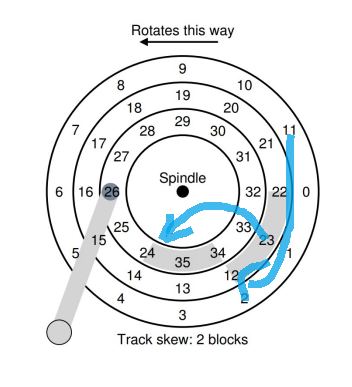
Make sure that sequential reads can be properly serviced even when crossing track boundaries.
Without such skew, the head would be moved to the next track but the desired next block
would have already rotated under the head.
일반적으로 Disk는 위 사진과 같이 생겼다.
앞장에는 numbering 할 때 11 => 12, 23 => 24 이 inner track 으로 접근하는 방식으로 그 다음 number가
inner track 으로 간 다음에 바로 옆에 존재한다.
그러나 11에서 12를 놓게 되는 동안에 15가 놓이게 되는 경우가 존재한다. (Track skew)
어느정도의 skew가 되어서 11 => 12로 배치가 되고 23 => 24 또한 skew 되서 배치된다.
그러나 Software 입장에서 36 Sectors 는 논리적으로 나눠서 0, 1, ..., 35 까지 볼 수 있다.
0: track index 0 의 0 1 : track index 0 의 1 2 : track index 0 의 2 ...
track skew는 OS blind 함
=> Inside disk로 내부적으로 disk가 track skew를 해결한다.
Multi-zoned

밖에 있는 track이 안에있는 track보다 저장할 게 많음. (밖 : 12,안 : 8)
밖에 있는 존, 안에 있는 존 이렇게 나누며 트랙이 여러개 있다.
sector 갯수는 고정이며 outer 갯수 N, inner 갯수 M 일때 N > M 이 성립한다.
Cache

Write-Back 같은 경우는 공간이 존재해야 하는데 없으면 Eviction, 있으면 write 한다.
I/O Time : Doing The Math
I/O Time :

I/O Rate :

아래 사진은 4KB Random Write에 대한 예시이다.


아래 사진은 Sequential Write 에 대한 예시이다.


Random 하게 4 KB를 작성한 경우와 Sequential 하게 100 MB를 작성한 경우다.
눈에 띄게도 Sequential 하게 작성한 경우가 Random 하게 작성한 경우보다 I/O Rate가 높게 나오는 것을 볼 수 있다.
즉, throughput이 좋아지는 것을 알 수 있다. (거의 maximum가 나옴)
따라서 sequential 할 때 write할 때 throughtput 이 좋아진다.
Cheetah, Barracuda 를 비교해볼 때 용량이 클 수록 I/O Rate 가 낮은것을 확인할 수 있다.
이때 Capacity 가 적은 대신에 Performance 를 선택하던가, Performance 가 적은 대신에
Capacity 를 선택할 수 있다.
Random 하게 데이터가 막 산재되어 있으면 Arm 입장에서 왔다갔다 움직이는데 그만큼 seek가 많아진다.
작은 data, 큰 data 등을 한번에 쓰는게(Sequential) 결국 더 빠르다!
Disk Scheduling
오늘 Disk Scheduling 을 배우면서 뭔가 낯설지가 않았다.
왜냐면 하계 대학생 S/W 알고리즘 역량 강화 특강에서 실전 문제로 Disk Scheduling 문제를 풀어본 적이
있기 때문이다.

FCFS 으로 Queue에 들어온 순서대로 처리하는 방식이다.

SSTF 으로 가장 근접한 순서대로 request를 처리하는 방식이다.
SJF scheduling과 동일하다고 보면 됨 (훨씬 실린더 움직임이 적어짐)
그러나 계속해서 근접한 request가 들어오게 되면 starvation이 발생하게 된다.

SCAN 으로 한방향으로 끝까지 가면 turn-around 하여 다른 끝 쪽으로 가는 방식이다.
SSTF 보다 효율적이며 elevator algorithm 이라고 불린다.

C-SCAN 으로 SCAN 보단 uniform한 wait time을 제공한다.
끝에 도달하면 맨 앞으로 돌아가게 된다.
Treats the cylinders as a circular list that wraps around from the last cylinder to the first one.

C-LOOK 으로 C-SCAN 보다 실린더 움직임이 적어진 것을 알 수 있다.
Arm이 last request 가 되면 즉시 앞에 존재하는 request 로 이동하여 처리해가는 방식이다.
SSTF 이 가장 많이 쓰인다고 한다.
SCAN, C-SCAN 은 부하가 많은 시스템에서 더 나은 성능을 발휘한다.
I/O merging
Queue 에서 순서대로 33, 8, 34 에 대한 request 가 1 개씩 push 될 때
33 => 34 를 읽는게 더 효율적이므로 봐서 2개의 request로 바꾼다. (seek time을 줄일 수 있음)
이러한 병합 작업은 드라이브 안에서 처리해준다.

FCFS, SSTF, SCAN, C-LOOK 에 대한 구현 코드는 다음과 같다.
C-LOOK 은 진행방향을 좌측으로 고정하여 위에 사진과 결과가 다르다.
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
const int MAX = 100000;
const int MAXN = 100000;
const int MAXB = 1000;
const int DIV = 100;
static int track_size;
static int track_head;
static int req_q[MAX];
static int req_size;
static int req_idx;
struct Node {
int val, idx;
Node* prev, * next;
Node* alloc(int _val, int _idx, Node* _prev, Node* _next) {
val = _val, idx = _idx;
prev = _prev, next = _next;
if (next) next->prev = this;
return this;
}
} buf[MAXN], bucket[MAXB];
int bCnt, bucketCnt[MAXB];
int tSize, tHead, lookOp;
int front, back;
int queue[MAX], visited[MAX], tail[MAXB];
void init(int track_size, int head) {
// TO DO
tSize = track_size, tHead = head;
lookOp = front = back = bCnt = 0;
for (int i = 0; i < MAXB; i++) {
bucketCnt[i] = 0;
bucket[i].next = 0;
bucket[i].val = -1;
}
for (int i = 0; i < track_size; i++) {
visited[i] = 0;
}
}
void request(int track) {
// TO DO
int index = track / DIV;
bucketCnt[index]++;
Node* ptr = &bucket[index];
while (ptr->next) {
if (ptr->next->val > track) break;
ptr = ptr->next;
}
// 끝부분에 data가 없는 경우 tail 값 설정
if (ptr->next == 0) tail[index] = track;
ptr->next = buf[bCnt++].alloc(track, index, ptr, ptr->next);
queue[back++] = track;
}
int fcfs() { // 요청된 순서대로 처리
int track_no = -1; // TO DO : Need to be changed
// order 별로 값 가져오기
while (visited[queue[front]]) {
front++;
}
track_no = queue[front++];
visited[track_no] = 1;
tHead = track_no;
// remove the data
int index = track_no / DIV;
Node* ptr = &bucket[index];
while (ptr->next) {
ptr = ptr->next;
if (ptr->val == track_no) break;
}
ptr->prev->next = ptr->next;
if (ptr->next) ptr->next->prev = ptr->prev;
// data tail 부분이 제거되는 경우
else {
tail[index] = ptr->prev->val;
}
bucketCnt[index]--;
return track_no;
}
int sstf() { // 현재 Head 위치를 기준으로 탐색 거리가 가장 짧은 요청 처리
int track_no = -1; // TO DO : Need to be changed
int index = tHead / DIV;
int gap = 100001;
// tHead에 속한 bucket에 값이 존재하는 경우
if (bucketCnt[index]) {
// 현재 bucket에 있는 gap을 추려낸다
Node* ptr = &bucket[index];
while (ptr->next) {
ptr = ptr->next;
int tmp = tHead - ptr->val < 0 ? ptr->val - tHead : tHead - ptr->val;
if (tmp < gap) {
gap = tmp;
track_no = ptr->val;
}
else break;
}
}
// 위아래 bucket에 존재하는 gap 값 또한 추린다
for (int i = index - 1; i >= 0; i--) {
if (bucketCnt[i]) {
int tmp = tHead - tail[i];
if (tmp <= gap) {
gap = tmp;
track_no = tail[i];
}
break;
}
}
for (int i = index + 1; i < tSize / DIV; i++) {
if (bucketCnt[i]) {
Node* ptr = &bucket[i];
ptr = ptr->next;
int tmp = ptr->val - tHead;
if (tmp < gap) {
gap = tmp;
track_no = ptr->val;
}
break;
}
}
// remove the data
visited[track_no] = 1;
tHead = track_no;
index = track_no / DIV;
Node* ptr = &bucket[index];
while (ptr->next) {
ptr = ptr->next;
if (ptr->val == track_no) break;
}
ptr->prev->next = ptr->next;
if (ptr->next) ptr->next->prev = ptr->prev;
// data tail 부분이 제거되는 경우
else {
tail[index] = ptr->prev->val;
}
bucketCnt[index]--;
return track_no;
}
int scan() {
int track_no = -1; // TO DO : Need to be changed
int index = tHead / DIV;
// Search the left
if (lookOp == 0) {
int gap = 100001;
Node* ptr = &bucket[index];
// 현재 Bucket에 존재하는 경우
if (ptr->next) {
while (ptr->next) {
ptr = ptr->next;
int tmp = tHead - ptr->val;
if (tmp > 0 && tmp < gap) {
gap = tmp;
track_no = ptr->val;
}
else break;
}
}
// 현재 Bucket에 존재하지 않는 경우
if (track_no == -1) {
for (int i = index - 1; i >= 0; i--) {
if (bucketCnt[i]) {
gap = tHead - tail[i];
track_no = tail[i];
break;
}
}
}
}
// Search the right
else {
int gap = 100001;
Node* ptr = &bucket[index];
// 현재 Bucket에 존재하는 경우
if (ptr->next) {
while (ptr->next) {
ptr = ptr->next;
int tmp = ptr->val - tHead;
if (tmp > 0 && tmp < gap) {
gap = tmp;
track_no = ptr->val;
break;
}
}
}
// 현재 Bucket에 존재하지 않는 경우
if (track_no == -1) {
for (int i = index + 1; i < tSize / DIV; i++) {
if (bucketCnt[i]) {
Node* ptr = &bucket[i];
ptr = ptr->next;
int tmp = ptr->val - tHead;
if (tmp < gap) {
gap = tmp;
track_no = ptr->val;
}
break;
}
}
}
}
if (track_no == -1) { // 발견하지 못한 경우
lookOp = (lookOp + 1) % 2;
track_no = scan();
}
else {
// remove the data
visited[track_no] = 1;
tHead = track_no;
index = track_no / DIV;
Node* ptr = &bucket[index];
while (ptr->next) {
ptr = ptr->next;
if (ptr->val == track_no) break;
}
ptr->prev->next = ptr->next;
if (ptr->next) ptr->next->prev = ptr->prev;
// data tail 부분이 제거되는 경우
else {
tail[index] = ptr->prev->val;
}
bucketCnt[index]--;
}
return track_no;
}
int clook() {
int track_no = -1; // TO DO : Need to be changed
int index = tHead / DIV;
// Search the left
int gap = 100001;
Node* ptr = &bucket[index];
// 현재 Bucket에 존재하는 경우
if (ptr->next) {
while (ptr->next) {
ptr = ptr->next;
int tmp = tHead - ptr->val;
if (tmp > 0 && tmp < gap) {
gap = tmp;
track_no = ptr->val;
}
else break;
}
}
// 현재 Bucket에 존재하지 않는 경우
if (track_no == -1) {
for (int i = index - 1; i >= 0; i--) {
if (bucketCnt[i]) {
gap = tHead - tail[i];
track_no = tail[i];
break;
}
}
}
// 존재하지 않는 경우 우측 끝으로 돌아감
if (track_no == -1) {
for (int i = tSize / DIV - 1; i >= 0; i--) {
if (bucketCnt[i]) {
track_no = tail[i];
break;
}
}
}
// remove the data
visited[track_no] = 1;
tHead = track_no;
index = track_no / DIV;
ptr = &bucket[index];
while (ptr->next) {
ptr = ptr->next;
if (ptr->val == track_no) break;
}
ptr->prev->next = ptr->next;
if (ptr->next) ptr->next->prev = ptr->prev;
// data tail 부분이 제거되는 경우
else {
tail[index] = ptr->prev->val;
}
bucketCnt[index]--;
return track_no;
}
static void load_data()
{
printf("Track Size : ");
scanf("%d", &track_size);
printf("Track Head : ");
scanf("%d", &track_head);
printf("Request Size : ");
scanf("%d", &req_size);
printf("\n=====> ");
for (register int i = 0; i < req_size; ++i) scanf("%d", &req_q[i]);
printf("\n");
}
static void run()
{
init(track_size, track_head);
for (int i = 0; i < req_size; i++) {
request(req_q[i]);
}
// FCFS
printf("1. FCFS \n ");
for (int i = 0; i < req_size; i++) {
if (i == req_size - 1)
printf("%d\n\n", fcfs());
else
printf("%d => ",fcfs());
}
init(track_size, track_head);
for (int i = 0; i < req_size; i++) {
request(req_q[i]);
}
// SSTF
printf("2. SSTF \n ");
for (int i = 0; i < req_size; i++) {
if (i == req_size - 1)
printf("%d\n\n", sstf());
else
printf("%d => ", sstf());
}
init(track_size, track_head);
for (int i = 0; i < req_size; i++) {
request(req_q[i]);
}
// SCAN
printf("3. SCAN \n ");
for (int i = 0; i < req_size; i++) {
if (i == req_size - 1)
printf("%d\n\n", scan());
else
printf("%d => ", scan());
}
init(track_size, track_head);
for (int i = 0; i < req_size; i++) {
request(req_q[i]);
}
// C-LOOK
printf("4. C-LOOK \n ");
for (int i = 0; i < req_size; i++) {
if (i == req_size - 1)
printf("%d\n\n", clook());
else
printf("%d => ", clook());
}
}
int main()
{
load_data();
run();
return 0;
}

'학교에서 들은거 정리 > 운영체제' 카테고리의 다른 글
| File system Implementation (1) | 2021.12.01 |
|---|---|
| Files and Directories (0) | 2021.11.27 |
| Semaphore and Common Concurrency Problem (0) | 2021.11.18 |
| Conditional Variables (0) | 2021.11.12 |
| Lock based Data Structure (0) | 2021.11.11 |




