mojo's Blog
Subset sum, Clique 본문
Integer partitioning 어떻게 해결해야 할지에 대한 접근법을 들어보자.
1. Greedy strategy
예를 들어 S = {4, 5, 6, 7, 8} 가 있을 때, Greedy strategy 로는 solution을 찾을 수 없다.
2. Dynamic programming

To solve an instance of subset sum, need to calculate f(1, t).
Note that f(j, t) = f(j + 1, t) or f(j + 1, t - xj).
The boundary condition is f(l, t) = true if t = 0 or t = xl and false otherwise.
The running time is propotional to the number of different subproblems we need to solve.
경계 조건으로 f(l, t)가 의미하는 바는 xl = t 인지에 대한 것인데,
t = 0 이거나, t = xl 일 경우에 true가 되며 그 외의 경우에는 false가 된다.
Since j ranges from 1 to l and t ranges from 0 to the total weight W = (x1 + ... + xi),
the number of different subproblems is O(lW).
=> If W is polynomial in n, the total length of the input, then integer partitioning is in P.
당연하게도, W가 적당한 숫자 n이라면 이 문제는 polynomial time에 해결할 수 있다.
그러나 W가 다음과 같은 경우라면 어떨까?
If xi are given in binary then W can be exponentially large making the dynamic programming
approach to take exponential time.
Assueme each xi has b bits, so the total size of the input is n = bl.
If b = l = n^(1/2), then W = l*2^b = 2^(n^(1/2)) * n^(1/2)

다음과 같이 xi가 b bit으로 구성된 binary number일 경우에 x1, ..., xl 으로 주어진 input 에 대한
total size는 결국 n = b*l 이 된다.
여기서 b = l = n^(1/2) 일 경우에 결국 W = x1 + ... + xl = l * 2^b = 2^(n^(1/2)) * n^(1/2) 이다.
Example
A sequence a1, ..., an of integers is called superincreasing if each element ai is strictly greater
than the sum of all previous elements.
Show that subset sum can be solved in polynomial time (via greedy method) if S is superincreasing.
문제에 대한 이해가 필요해 보인다.
{1, 2, 4, 8, 16, 32, ... , 2^n} 에 대한 배열이 있다고 할 때,
(1) 2 > 1
(2) 4 > (1 + 2)
(3) 8 > (1 + 2 + 4)
...
(n) 2^n > (1 + 2 + 4 + ... + 2^(n-1))
임이 성립할 때 이를 superincreasing 이라고 부르며 이러한 배열에 대한 subset sum문제를 해결하는 것은
polynomial time에 해결이 가능하다고 한다.
이에 대한 증명을 알아보도록 하자.
Proof :
Let A be the subset, if there is one, which sums to t.
Let aj be the largest element of the superincreasing sequence such that aj ≤ t.
None of the numbers ai with i > j can be in A since they are all larger than t.
Similarly, all the numbers ai with i < j sum up to some value less than aj , so they alone can never
sum up to t.
Hence aj must be an element of A.
합이 t가 되도록 하는 subset A가 존재한다고 할 때, aj ≤ t 를 만족하는 가장 큰 원소인 aj를 생각해보자.
i > j 인 경우 => ai > t 를 만족하므로 t를 만족하지 못한다.
i < j 인 경우 => ai < t 를 만족하므로 이 또한 t를 만족하지 못한다.
Replace t by t − aj , and remove aj from the sequence.
Iterate until either t = 0, in which case we have found a solution, or until aj > t for all j,
in which case no solution exists.
즉, {1, 2, 5, 10, 20, 60, 150} 이 있고 k = 87 에 대해서 위 방법대로 찾는다고 한다면 다음과 같다.
(1) 150 > k 이므로 150 은 제외 대상이다. => { }
(2) 60 < k 이므로 60 은 포함 대상이며 k = k - 60 = 27 으로 바꾼다. => {60}
(3) 20 < k 이므로 20 은 포함 대상이며 k = k - 20 = 7 으로 바꾼다. => {20, 60}
(4) 10 > k 이므로 10은 제외 대상이다. => {20, 60}
(5) 5 < k 이므로 5 는 포함 대상이며 k = k - 5 = 2 으로 바꾼다. => {5, 20, 60}
(6) 2 = k 이므로 2 는 포함 대상이며 k = 0 으로 바꾼다. => {2, 5, 20, 60}
(7) t = 0 이 될 때까지 반복하였고 solution을 찾았다.
(t가 0이 아니며 모든 iteration 을 하였다면 그 경우는 solution을 발견하지 못한 것임)
If S = { 1, 2, 4, 8, · · ·},
this algorithm produces the subset corresponding to the binary expansion of t.
Example
A public-key cryptosystem provides an asymmetric pair of keys: a public and a private key.
Anyone can encrypt using the public key, but only the owner of the private key can
decrypt the message.
The following is a public-key cryptosystem based on subset sum.
대략 아래와 같이 public key를 통해 message를 암호화 하고 private key를 통해 오직 owner 만이
암호화된 message를 해독할 수 있다.이러한 과정이 subset sum을 기반으로 구성되었다고 한다.
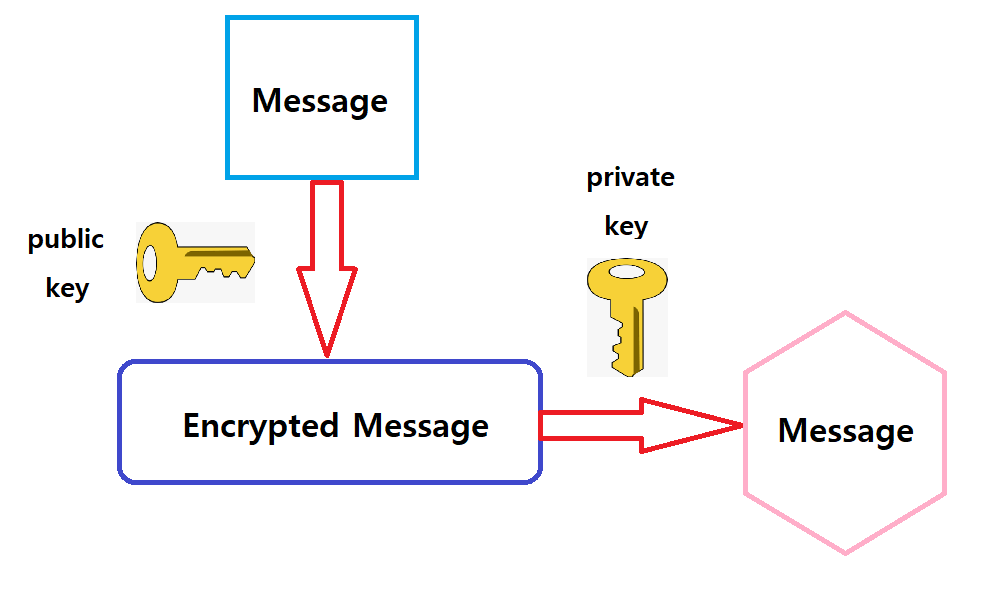
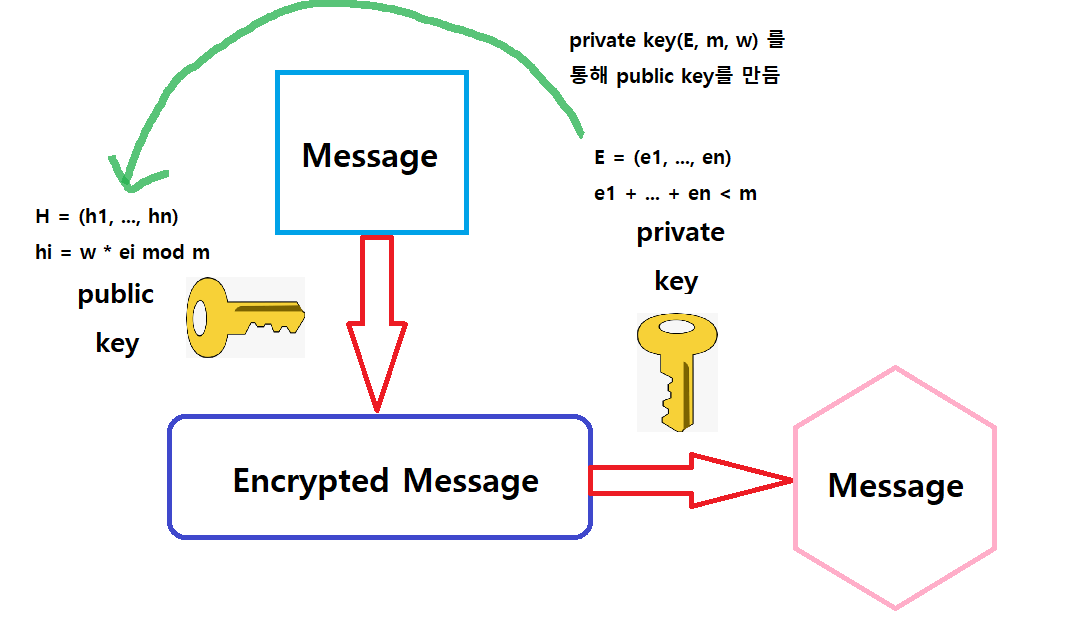
The private key consists of a superincreasing sequence E = ( e1, · · · , en ) of integers,
a modulus m greater than (e1 + ... + en) , and a multiplier w that is relatively prime to m.
The public key is a sequence H = ( h1, · · · , hn ) derived from the private key
via hi = w * ei mod m
정리해보면 다음과 같다.
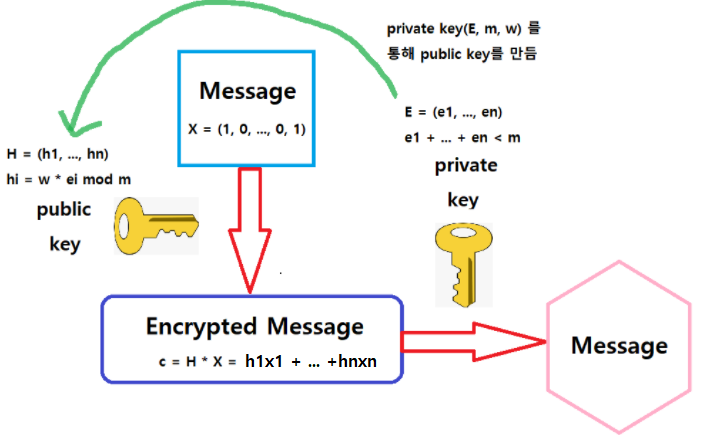
The encryption of an n-bit message X = (x1, · · · , xn) is the number
c = H · X = h1x1 + h2x2 + ... + hnxn.
Decrypting the message is solving c = H · X for X = {0, 1}^n which is equivalent to solving
subset sum for H with target sum c.
⇒ Impossible for any person to decrypt the message c.
On the other hand, the owner of the private key can calculate
w^(-1) · c = w^(-1) · H · X
≡ w^(-1) · w · E · X mod m
≡ E · X mod m
= E · X
E · X mod m = E · X 가 된 이유는 위에서 언급한 것 처럼 m > (e1 + ... + en) 이기 때문이다.
즉, H = w · E 임을 이용함으로써 w^(-1) · c = E · X 임을 알 수 있다.
This is an instance of subset sum for the superincreasing sequence E where the target sum is w^-1c.
We know this instance is in P.
To break this cryptosystem, suffices to find a relatively prime pair (w′, m′)
s.t. ai ≡ w′hi mod m′ is a superincreasing sequence, not necessarily the same as the original
sequence E, and m′ > a1 + a2 + ... an.
Then,
w′c = w′H · X
≡ A · X mod m′
= A · X
It was later proven that such (w′, m′) can be found in polynomial time which shows that
the described cryptosystem based on subset sum is not secure.
즉, polynomial time으로 (w', m') 을 찾을 수 있고 이는 즉, 암호가 뚫리는 상황이 발생한다.
따라서 subset sum을 기반으로 한 암호화 시스템이 안전하지 못하다는 것이 증명되었다.
Cliques
cliques 에 대해서 대충 알아보도록 하자.
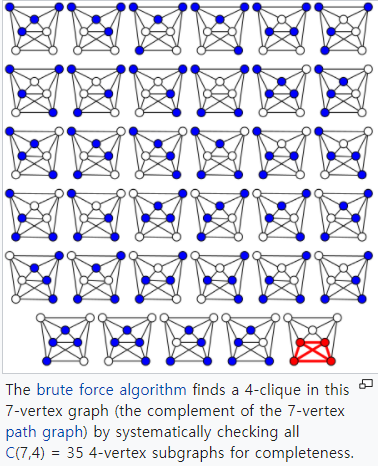
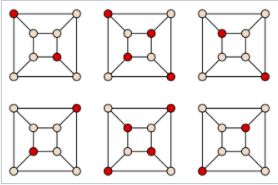
brute force algorithm 을 이용하여 4-clique를 찾는 예시이다.
7개의 정점 중에 4개의 정점을 사용한 것으로 7C4 = 35 개의 정점들에 대해서 서칭함으로써 찾아낼 수 있다고 한다.
이 문제는 딱 봐도 exponential한 time complexity 를 갖는 것으로 추정된다.
Given a graph G = (V, E), a subset S ⊆ V is independent if no two vertices in S are adjacent.
independent set
Input: A graph G and an integer k
Question: Does G have an independent set of size k or more?
A subset S ⊆ V is a vertex cover if for every edge e ∈ E, at least one of e’s endpoints is in S.
vertex cover
Input: A graph G and an integer k
Question: Does G have a vertex cover of size k or less?

S ⊆ V is a clique if every vertex in S is adjacent to every other, so that S forms a complete graph.
clique
Input: A graph G and an integer k
Question: Does G have a clique of size k or more?
Claim: The following are equivalent.
1. S is an independent set.
2. V − S is a vertex cover.
3. S is a clique in the complemented graph G¯ = (V, E¯) where two vertices are adjacent
if and only if they are not adjacent in G.
3번에서 그래프 G에서 인접하지 않을 경우 complement 한 G¯ 에 대해서 결국 인접함을 알 수 있다.
따라서 complement하여 clique를 알아낼 수 있다.
∃ an independent set of size ≥ k
⇔ ∃ a vertex cover of size ≤ n − k
⇔ ∃ a clique in G¯ of size ≥ k.
If k is a constant, can go through all nCk = O(n^k) possible sets of k vertices and check
whether they are independent, form vertex cover, or are a clique.
In other words, they are all in P.
However, k is part of the input.
E.g., if k = αn for some 0 < α < 1, then nCk grows exponentially wrt n.
In any case, they are all in NP.
nCk = n! / ((n - k)! * k!) 라는게 어마무시하기 때문에 이는 exponential 하게 증가하므로 결국 NP 이다.
independent set (exact version)
Input: A graph G and an integer k
Question: Does G’s largest independent set have size exactly k?
This version of the problem has a more complex logical structure and belongs to complexity
class somewhat higher than NP.
k 이상인 independent set 를 찾는 문제 보다 정확히 k 개인 independent set를 찾는게 더 어렵고 복잡한
logical structure를 사용하여 해결해야 한다.
즉, independent set가 정확히 k개 인지를 확인하는 문제는 NP 보다 더 어렵다고 할 수 있다.
'학교에서 들은거 정리 > 자동장치' 카테고리의 다른 글
| balanced k-coloring (0) | 2021.11.30 |
|---|---|
| Designing Reduction (0) | 2021.11.25 |
| 2-sat, Balancing Numbers (0) | 2021.11.16 |
| Satisfiability Problem (0) | 2021.11.11 |
| Duality, Reduction (0) | 2021.11.10 |




