mojo's Blog
Duality, Reduction 본문
Duality
Consider a directed graph G where each edge e has a nonnegative integer capacity c(e).
Goal is to arrange a flow from a source s to a destination t.
Flow consists of assigning an integer f(e) to each edge such that 0 ≤ f(e) ≤ c(e).
Goal is to maximize the total flow out of s and into t, called the value of the flow.
양의 정수를 갖는 간선 e의 capacity c(e)에 대해서 방향 그래프 G가 있다.
source "s"부터 destination "t"까지의 flow값을 최대로 하는 것이 문제이다.
max flow
Input : A network G where each edge has nonnegative integer capacity c(e).
Question : What is the maximum flow from s to t?
A flow f may be improved by adding another flow δ from s to t.
When does such δ exist?
유량 f를 증가시키기 위한 또다른 유량 δ에 대해서 고려해보도록 하자.
Define a residual network Gf where each edge has capacity cf(e) = c(e) - f(e).
We can increase the flow on edges with nonzero capacity in Gf.
기존에 있던 방향그래프 G에 대해서 capacity c(e)에서 flow f(e)를 뺀 값을 cf(e)라고 할 때,
각 간선이 cf(e)에 대해서 구성되어진 residual network Gf 를 통해서 유량 flow 값을 증가시킬 수 있다.
We can include a "reverse" edge e_ = (v, u) for each edge e = (u, v) of G without making the
flow negative, and give these reverse edges a capacity cf(e_) = f(e).
Given a flow f, call a path from s to t along edges with nonzero capacity in the residual network
Gf an augmenting path.
★ augmenting path?
residual network Gf 에서 s부터 t까지의 capacity가 0이 아닌 모든 간선들을 따라가는 path를 의미한다.
간선 e의 반대방향 e_ 에 대해서 cf(e_) = f(e) 에 대한 것을 살펴보도록 하자.

위 사진에서 동그라미를 친 간선 e를 고려해보자.
f(e) = 1 이고 residual network Gf 에서의 cf(e) = 0, cf(e_) = 1 임을 알 수 있다.
즉, cf(e_) = f(e) = 1이 성립하는 것을 알 수 있겠다.
※ Theorem 1
A flow f is maximal if and only if there is no augmenting path.
If there is an augmenting path, increasing/decreasing the flow along it produces
a new flow f' of greater value.
augmenting path가 없을때 유량 f가 최대라는 것을 증명해보도록 하자.
Proof :
Suppose an augmenting path δ exists.
Each edge of δ is either a forward edge e where f(e) < c(e) and f(e) can be increased,
or a reverse edge e_ and f(e) can be decreased.
Adding a unit of flow along δ gives a new flow f' where 0 ≤ f'(e) ≤ c(e) along every edge
and whose value is greater than that of f.

augmented path δ가 있다고 가정하면 각 간선 e에 대해서 e에 대한 flow는 증가할 것이고
반대방향의 간선 e_ 에 대해서 e에 대한 flow는 감소하게 된다.
위 그림처럼 forward edge e에 대해서 는 flow가 증가하였고 reverse edge e_ 에 대해서는
flow가 감소한 것을 알 수 있다.
Conversely, suppose there is a flow f' whose value is greater than that of f.
(위 상황과는 다르게 flow f'가 이전 flow f보다 항상 크다는 것을 감안함)
We can define a flow △ on Gf as follows:
△(e) = max(0, f'(e) - f(e)), △(e_) = max(0, f(e) - f'(e))
Easy to check that the total flow △ in and out of any vertex other than s or t is zero.
Moreover, if f'(e) > f(e), then
0 < △(e) = f'(e) - f(e) ≤ c(e) - f(e) = cf(e),
and if f'(e) < f(e), then
0 < △(e_) = f(e) - f'(e) ≤ f(e) = cf(e_).
△ is a legal flow on Gf, and has positive value equal to the value of f' minus that of f.
it is the augmenting path.
f(e) - f'(e) ≤ f(e) = cf(e_) 에서 f(e) = cf(e_) 에 대한 것을 살펴보려고 한다.
cf(e_) = c(e_) - f(e_) 이고, reverse edge e_에 대한 capacity c(e_) = 0 이므로
cf(e_) = -f(e_) 이다.
f(e_)는 reverse edge e_에 대한 flow 인데
"edge e에 대한 flow가 증가하면 reverse edge e_에 대한 flow가 감소한다"
를 이용하면 f(e) = -f(e_) 임을 짐작할 수 있겠다.
즉, cf(e_) = -f(e_) = f(e) 임을 알 수 있다.
To check if a flow f is maximal or not, need to only check if there is a path in Gf from s to t.
Recalculating the residual capacities in Gf and continuing until no augmenting paths remain
will end at the maximal flow.
(This is known as the Ford-Fulkerson algorithm!)
The value of the flow increases by at least one each time, so the number of iterations is
at most the sum of all capacities.
Claim : Total number of iterations is polynomial in n.
결론으로 최대 flow를 구하기 위해서는
① Gf 즉, source "s" 에서 destination "t" 로 가는 augmenting path 가 있는지 확인
(없으면 최대 flow를 구함, 있으면 다음 step 이동)
② 있을 경우 flow값을 update 한 후에 다시 Gf 를 recalculate 한다.
③ recalculate 한 Gf 에 대해서 ① 로 이동한다.
이러한 알고리즘을 Ford-Fulkerson algorithm 이라고 한다.
해당 알고리즘은 적어도 한번씩 iteration을 돌 때마다 flow값이 증가하는 것을 확인할 수 있다.
즉, worst case로 flow값이 1씩 증가한다고 할 때, O(max_flow * E) 임을 알 수 있겠다.
따라서 polynomial time 임이 증명되었다.
min cut
Input: A weighted graph G and two vertices s, t.
Question: What is the weight of the minimum cut that separates s from t ?
Note
value(max flow) ≤ weight(min cut)
min cut에 대한 간단한 예제를 보도록 하자.

다음과 같은 Network Graph G가 있다.

아래의 Gf' 를 보면 s에서 t로 가는 augmented path가 존재하지 않음을 알 수 있다.
(A => B로 갈 수 없으며 동시에 C => D로 갈 수 없는 상태이므로)
이 경우에 cf(e) = 0 간선 e를 적절하게 잘라내어 start 정점과 end 정점이 묶이지 않도록 하는 2개의 그룹으로
만들어내는 것을 cut 한다고 한다.
즉, A => B로 가는 경우와 C => D로 가는 경우를 잘라낸다면 {S, A, C}, {B, D, T} 2개의 그룹으로 형성된다.
이런식으로 2개의 그룹을 형성시킬 수 있도록 min cut 하는 방법에 대해서 알아보도록 한다.
How about value(max flow) = weight(min cut)?
If f is a maximal flow, then there is no augmenting path.
So s is cut off from t by a set of edges whose residual capacity is zero.
S = the set of vertices reachable from s along edges with nonzero cf
T = the remaining set of vertices including t.
즉, S는 정점 s로 부터 cf(e) = c(e) - f(e) > 0 인 정점들의 set 이며T는 S를 제외한 나머지 정점들의 set 이다.
Since each edge that crosses from S to T has cf(e) = 0, we get f(e) = c(e).
The weight of the cut between S and T is the total weight of all theses edges andit equals the value of f.
So, ∃ a cut whose weight equals the maximum flow.
But any cut has weight at least this large, so it must be the cut with the minimum value.
max flow ∈ P ⇒ min cut ∈ P.
min cut is the best possible upper bound on max flow.
max flow is the best possible lower bound on min cut.
This relationship is an example of duality.
즉, min cut은 max flow의 가능한 상한이며 max flow는 min cut의 가능한 하한이다.
min cut과 max flow는 따라서 duality 즉, 연관된 문제이며 Polynomial algorithm 이다.
max flow is a constrained optimization problem that has a "mirror image" which is a minimization problem of min cut.
Reductions
Transformation or reduction of one problem to another is a fundamental idea in computational complexity.
max bipartite matching
Input : A bipartite graph G.
Question: What is the maximum matching?
이 문제는 백준 11375번: 열혈강호 (acmicpc.net) 를 통해서 먼저 감을 잡아보도록 한다.
#define _CRT_SECURE_NO_WARNINGS
#include <queue>
#include <iostream>
#include <vector>
using namespace std;
const int S = 0, E = 2001;
int capacity[2022][2022], flow[2022][2022], d[2022];
vector<int> v[2022];
void initialize(int N, int M)
{
int i;
// from dummy(start) to employee
// dummy(start) : 0
for (i = 1; i <= N; i++) {
v[S].push_back(i), v[i].push_back(S);
capacity[S][i] = 1;
}
// from job to dummy(end)
// dummy(end) : E(2001)
for (i = 1001; i <= 1000 + M; i++) {
v[i].push_back(E), v[E].push_back(i);
capacity[i][E] = 1;
}
}
void fill_d(int d[], int size)
{
int i;
for (i = 0; i <= size; i++)
d[i] = -1;
}
int maxFlow(int start, int end)
{
int i, cur, max_flow, min_flow;
max_flow = 0;
while (1) {
fill_d(d, end);
queue<int> Q;
Q.push(start);
while (!Q.empty()) {
cur = Q.front(), Q.pop();
for (int next : v[cur]) {
if (d[next] == -1 && capacity[cur][next] - flow[cur][next] > 0) {
Q.push(next), d[next] = cur;
if (next == end)
break;
}
}
}
if (d[end] == -1) return max_flow;
min_flow = 1000000000;
for (i = end; i != start; i = d[i]) {
min_flow = min(min_flow, capacity[d[i]][i] - flow[d[i]][i]);
}
max_flow += min_flow;
for (i = end; i != start; i = d[i]) {
flow[d[i]][i] += min_flow;
flow[i][d[i]] -= min_flow;
}
}
}
int main()
{
ios_base::sync_with_stdio(false); cin.tie(0); cout.tie(0);
int N, M, job_cnt, job;
cin >> N >> M;
initialize(N, M);
for (int i = 1; i <= N; i++) {
cin >> job_cnt;
for (int j = 0; j < job_cnt; j++) {
cin >> job;
v[i].push_back(1000 + job), v[1000 + job].push_back(i);
capacity[i][1000 + job] = 1;
}
}
cout << maxFlow(S, E);
return 0;
}
We can transform an instance of max bipartite matching into an instance of max flow.
Turn each compatible couple (u, v) into a directed edge u -> v pointing from left to right.
Add two vertices such that edges s -> u for each u on the left, and v -> t for each t on the right.
Finally, give every edge in this network a capacity 1.
굉장히 중요한 스킬이 나왔다.
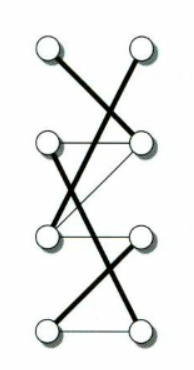
다음과 같은 bipartite graph G 를 고려한다.
여기서 왼쪽 정점들을 u, 오른쪽 정점들을 v라 하고 양 옆에 정점을 추가해준다.

음? 결국 이전에 봤던 max flow 문제가 되버린 것이다.
즉, bipartite graph 에 대해서 maximum matching 문제는 결국 max flow 문제에 속해 있다는 것을
알 수 있고 이는 Polynomial time 으로 해결이 가능하다는 것을 알 수 있다.
max bipartite matching is solved by this reduction to max flow.
max flow is in P, so is max bipartite matching.
In particular, max bipartite matching is no harder than max flow!
max bipartite matching ≤ max flow.
Just as reduction A ≤ B shows that A is at most as hard as B, it also shows that
B is at least as hard as A.
'학교에서 들은거 정리 > 자동장치' 카테고리의 다른 글
| balanced k-coloring (0) | 2021.11.30 |
|---|---|
| Designing Reduction (0) | 2021.11.25 |
| Subset sum, Clique (0) | 2021.11.18 |
| 2-sat, Balancing Numbers (0) | 2021.11.16 |
| Satisfiability Problem (0) | 2021.11.11 |




