mojo's Blog
[백준 1761] 정점들의 거리 본문
문제 링크 => 1761번: 정점들의 거리 (acmicpc.net)
1761번: 정점들의 거리
첫째 줄에 노드의 개수 N이 입력되고 다음 N-1개의 줄에 트리 상에 연결된 두 점과 거리를 입력받는다. 그 다음 줄에 M이 주어지고, 다음 M개의 줄에 거리를 알고 싶은 노드 쌍이 한 줄에 한 쌍씩
www.acmicpc.net
정점과 정점사이의 거리를 구하는 문제이다.
이 문제 역시 LCA 문제인데 다음과 같은 그림을 통해 해당 수식을 이해하기 전에 간단하게 배열들에 대한 설명을 하자면 다음과 같다.
- parent[x][y] => x 노드의 2^y 의 부모
- depth[x] => x 노드의 깊이, 보통 1을 0으로 잡는다.
- path[x] => 1부터 x까지 연결된 노드의 길이
그렇다면 두 노드를 LCA를 통해 어떻게 구할지는 다음 그림을 보면 된다.
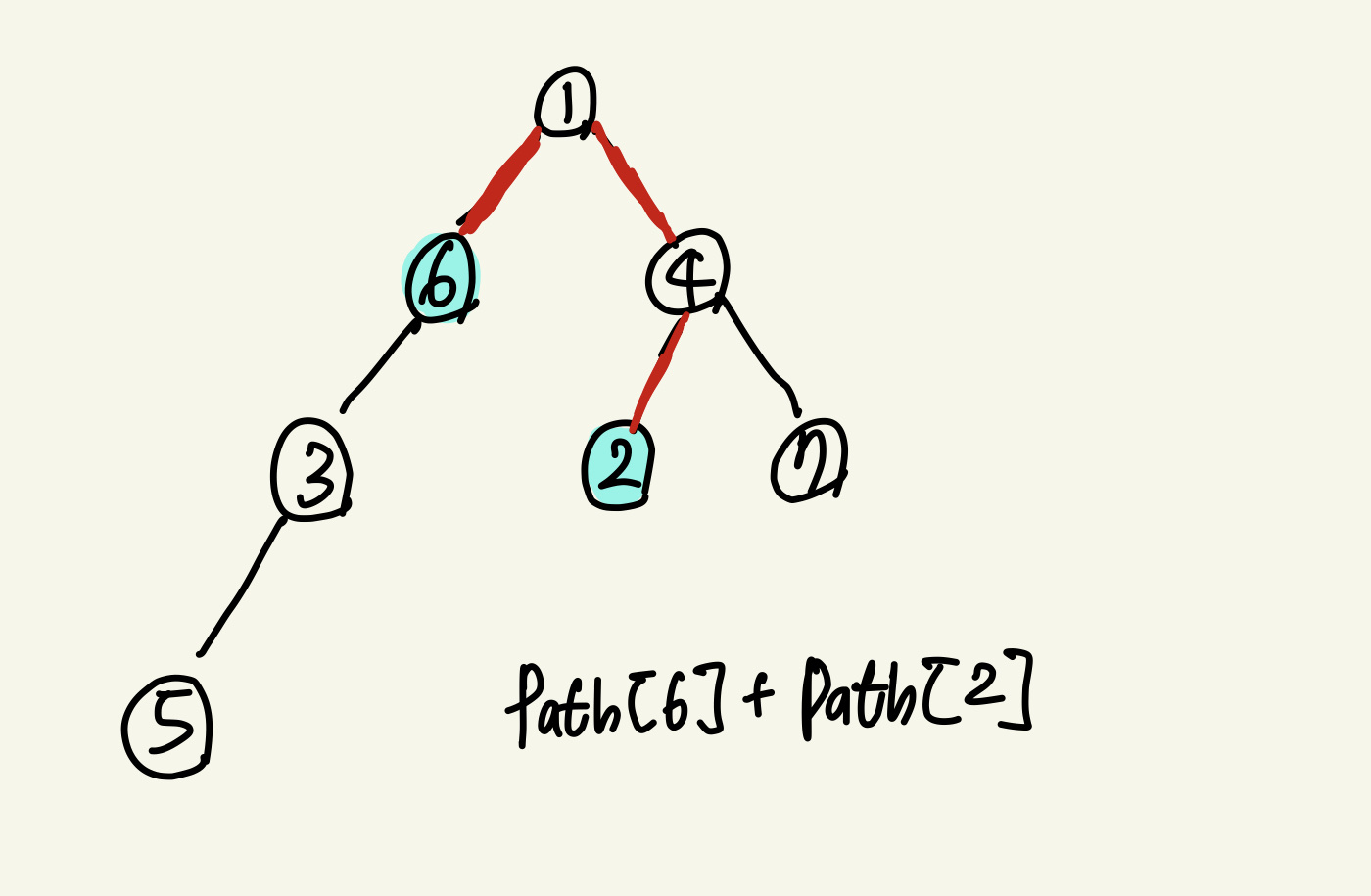
문제에 주어진 예시중에 2 노드와 6 노드의 거리를 구하는 방법이다.
이때는 단순하게 path[2] + path[6] 이 정답이지만 다른 경우를 살펴보려고 한다.
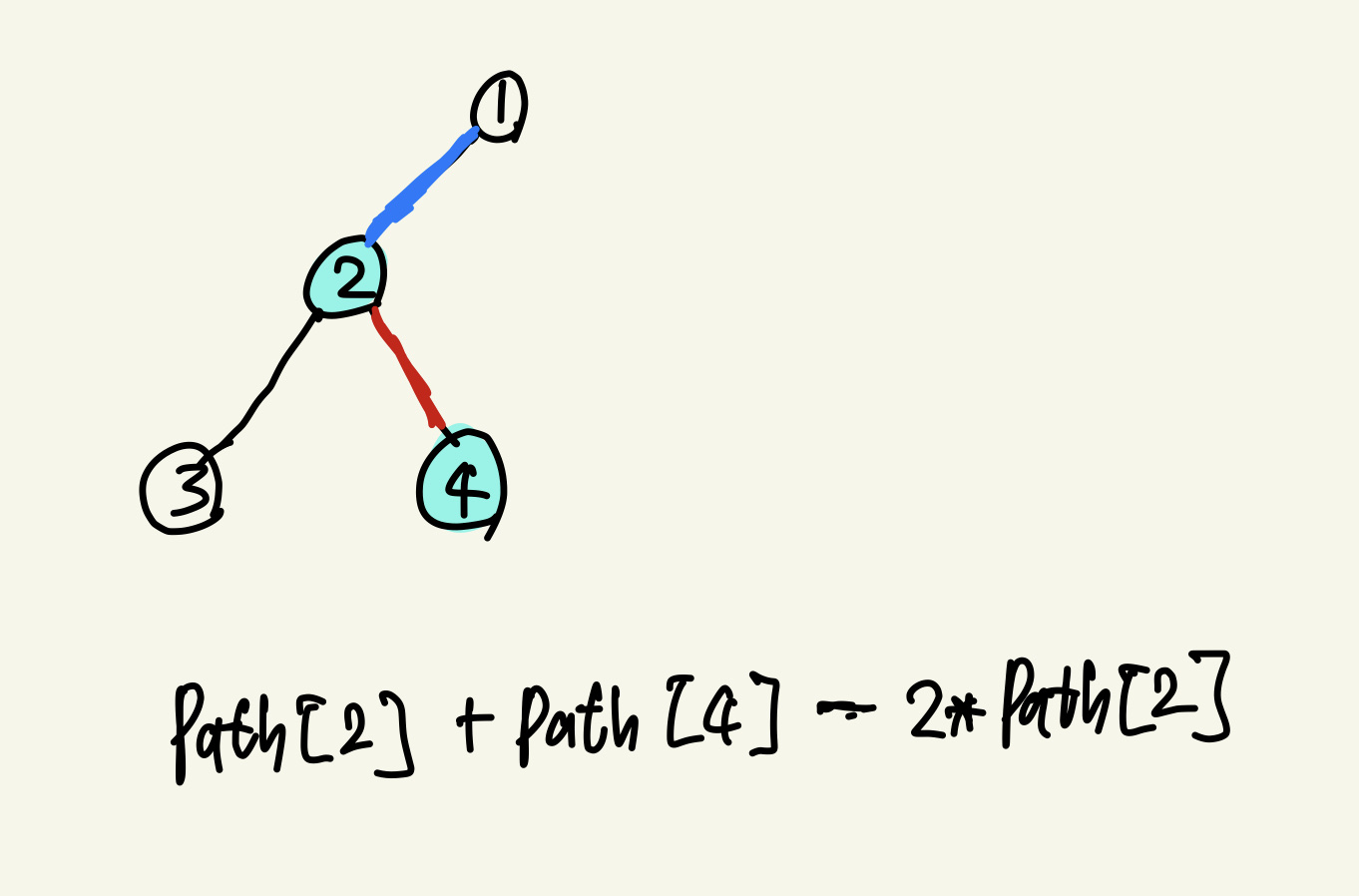
이러한 경우 2 노드와 4 노드의 거리를 구할때 겹치는 부분이 2개가 존재한다.
이때, LCA(2, 4) = 2 임을 이용하여 path[2] + path[4] - 2*path[2] 가 된다.
이를 일반화하면 다음과 같은 수식이 만들어진다.
임의의 노드 x, y가 주어질 때, x, y 사이의 거리를 distance라고 할 경우
distance = path[x] + path[y] - 2*path[LCA(x,y)]
풀이 code
#define _CRT_SECURE_NO_WARNINGS
#include <string>
#include <stdio.h>
#include <math.h>
#include <iostream>
#include <vector>
#include <algorithm>
#include <map>
#include <queue>
#include <set>
#include <stack>
#include <time.h>
#define INF 100000000
#define endl '\n'
#define MOD 1000000009
#define ll long long
using namespace std;
int n;
vector<pair<int,int>> v[40001];
bool visited[40001];
int parent[40001][21], depth[40001], path[40001];
void compose_LCA(int start) {
queue<int> q;
q.push(start);
visited[start] = true;
while (!q.empty()) {
int x = q.front();
q.pop();
for (int i = 0; i < v[x].size(); i++) {
int next = v[x][i].first;
int dist = v[x][i].second;
if (!visited[next]) {
visited[next] = true;
parent[next][0] = x;
depth[next] = depth[x] + 1;
path[next] = path[x] + dist;
q.push(next);
}
}
}
for (int j = 1; j <= 20; j++) {
for (int i = 1; i <= n; i++) {
parent[i][j] = parent[parent[i][j - 1]][j - 1];
}
}
}
int LCA(int x, int y) {
if (depth[x] > depth[y]) swap(x, y);
for (int i = 20; i >= 0; i--) {
if (depth[y] - depth[x] >= (1 << i)) {
y = parent[y][i];
}
}
if (x == y) return x;
for (int i = 20; i >= 0; i--) {
if (parent[x][i] != parent[y][i]) {
x = parent[x][i], y = parent[y][i];
}
}
return parent[x][0];
}
int main() {
ios_base::sync_with_stdio(false); cin.tie(0); cout.tie(0);
cin >> n;
for (int i = 0; i < n - 1; i++) {
int a, b, dist;
cin >> a >> b >> dist;
v[a].push_back({ b,dist });
v[b].push_back({ a,dist });
}
compose_LCA(1);
int m;
cin >> m;
for (int i = 0; i < m; i++) {
int x, y;
cin >> x >> y;
cout << path[x] + path[y] - 2 * path[LCA(x, y)] << endl;
}
return 0;
}
'백준 > Graph' 카테고리의 다른 글
| [백준 2637] 장난감 조립 (0) | 2021.07.27 |
|---|---|
| [백준 6543] 그래프의 싱크 (0) | 2021.07.26 |
| [백준 11438] LCA 2 (0) | 2021.07.20 |
| [백준 11437] LCA (0) | 2021.07.20 |
| [백준 19535] ㄷㄷㄷㅈ (0) | 2021.07.17 |
Comments




