mojo's Blog
2021 카카오 인턴십 문제 리뷰 본문
1. 숫자 문자열과 영단어
문제 링크 : 코딩테스트 연습 - 숫자 문자열과 영단어 | 프로그래머스 (programmers.co.kr)
코딩테스트 연습 - 숫자 문자열과 영단어
네오와 프로도가 숫자놀이를 하고 있습니다. 네오가 프로도에게 숫자를 건넬 때 일부 자릿수를 영단어로 바꾼 카드를 건네주면 프로도는 원래 숫자를 찾는 게임입니다. 다음은 숫자의 일부 자
programmers.co.kr
단순 문자열 구현 문제이다.
숫자와 영단어가 섞인 문자열이 주어질 때 이를 숫자로 나타내도록 구현해야 한다.
우선, 숫자는 20억 이하의 숫자이므로 자연스럽게 int 형임을 확인할 수 있다.
문자열을 인덱스 i 를 이용하여 처음부터 접근할 때 숫자인 경우와 영단어인 경우를 구분한다.
그리고 숫자를 문자열 result 로 하여 나중에 int 형으로 변환하도록 설정하였다.
영단어를 구분할 때는 s.substr(i, n) 과 같이 구분하였다. (이때 n은 영단어의 길이)
- s[i] 가 숫자인 경우 : 숫자 문자를 result 에 붙여준다.
- s[i] 가 영단어인 경우 : 영단어와 매치되는 숫자 문자를 result 에 붙여준다.
마지막으로 answer = stoi(result) 를 통해 숫자로 변환해서 반환하면 된다.
문제 풀이 코드
#include <string>
#include <vector>
using namespace std;
int solution(string s) {
int answer = 0;
string result = "";
for (int i = 0; i < s.size(); i++) {
if (s.substr(i, 4) == "zero") result += "0", i += 3;
else if (s.substr(i, 3) == "one") result += "1", i += 2;
else if (s.substr(i, 3) == "two") result += "2", i += 2;
else if (s.substr(i, 5) == "three") result += "3", i += 4;
else if (s.substr(i, 4) == "four") result += "4", i += 3;
else if (s.substr(i, 4) == "five") result += "5", i += 3;
else if (s.substr(i, 3) == "six") result += "6", i += 2;
else if (s.substr(i, 5) == "seven") result += "7", i += 4;
else if (s.substr(i, 5) == "eight") result += "8", i += 4;
else if (s.substr(i, 4) == "nine") result += "9", i += 3;
else if (s[i] >= '0' && s[i] <= '9') result += s[i];
}
answer = stoi(result);
return answer;
}
2. 거리두기 확인하기
문제 링크 : 코딩테스트 연습 - 거리두기 확인하기 | 프로그래머스 (programmers.co.kr)
코딩테스트 연습 - 거리두기 확인하기
[["POOOP", "OXXOX", "OPXPX", "OOXOX", "POXXP"], ["POOPX", "OXPXP", "PXXXO", "OXXXO", "OOOPP"], ["PXOPX", "OXOXP", "OXPOX", "OXXOP", "PXPOX"], ["OOOXX", "XOOOX", "OOOXX", "OXOOX", "OOOOO"], ["PXPXP", "XPXPX", "PXPXP", "XPXPX", "PXPXP"]] [1, 0, 1, 1, 1]
programmers.co.kr
전형적인 그래프 탐색 문제이다.우선, 문제에 주어진 조건을 파악해보자.
참고 : 두 테이블 T1, T2가 행렬 (r1, c1), (r2, c2)에 각각 위치하고 있다면,
T1, T2 사이의 맨해튼 거리는 |r1 - r2| + |c1 - c2|
(1) 거리두기를 잘 한 경우

위 사진은 두 사람 사이에 벽이 존재하는 경우다.
두 사람 사이에 벽이 존재하여 서로 이동하여 볼 수 없는 상황으로 즉, 거리두기를 잘 한 것이다.

위 사진은 두 사람 사이에 벽이 존재하지 않은 경우다.
두 사람 사이에 빈 테이블이 두 개 존재하여 서로 이동할 수 있지만 두 사람 사이의 맨해튼 거리가 3 이므로 2를 넘어서기 때문에 거리두기를 잘 한 것이다.
(2) 거리두기를 못 한 경우

위 사진은 두 사람 사이에 빈 테이블이 존재하는 경우다.
두 사람 사이에 빈 테이블이 존재하므로 서로 이동하여 볼 수 있는 경우이다.
즉, 두 사람 사이의 맨해튼 거리가 2 이므로 거리두기를 못 한 것이다.

위 사진은 왼쪽 윗 사람이 아래로 이동하고 오른쪽으로 이동할 경우 만나게 되므로 거리두기를 못 한 것이다.
정리하면 특정 사람을 기준으로 하여 이동할 수 있는 모든 경우를 탐색하여 맨해튼 거리가 2 이내에 사람을 발견하면 거리두기를 못한 경우고 그 외에는 거리두기를 잘한 경우다.
즉, bfs 를 이용하여 해결할 수 있다.
문제 풀이 코드
#include <string>
#include <vector>
#include <queue>
using namespace std;
bool visited[5][5];
int dx[4] = { 1, -1, 0, 0 };
int dy[4] = { 0, 0, 1, -1 };
void convert(vector<string> place, char Map[][5]) {
for (int i = 0; i < place.size(); i++) {
for (int j = 0; j < place[i].size(); j++) {
Map[i][j] = place[i][j];
}
}
}
void init() {
for (int i = 0; i < 5; i++) {
for (int j = 0; j < 5; j++) {
visited[i][j] = false;
}
}
}
bool check(int start_x, int start_y, char Map[][5]) {
queue<pair<pair<int, int>, int>> Q;
Q.push({ {start_x, start_y}, 0 });
visited[start_x][start_y] = true;
while (!Q.empty()) {
int x = Q.front().first.first, y = Q.front().first.second;
int t = Q.front().second;
Q.pop();
if (t != 0 && Map[x][y] == 'P')
return false;
if (t == 2)
continue;
for (int i = 0; i < 4; i++) {
int next_x = x + dx[i], next_y = y + dy[i];
if (next_x >= 0 && next_x < 5 && next_y >= 0 && next_y < 5) {
if (Map[next_x][next_y] != 'X' && !visited[next_x][next_y]) {
Q.push({ {next_x, next_y}, t + 1 });
visited[next_x][next_y] = true;
}
}
}
}
return true;
}
int go(char Map[][5]) {
for (int i = 0; i < 5; i++) {
for (int j = 0; j < 5; j++) {
if (Map[i][j] == 'P') {
init();
if (!check(i, j, Map))
return 0;
}
}
}
return 1;
}
vector<int> solution(vector<vector<string>> places) {
vector<int> answer;
char Map[5][5];
for (int i = 0; i < places.size(); i++) {
convert(places[i], Map);
answer.push_back(go(Map));
}
return answer;
}
3. 표 편집
문제 링크 : 코딩테스트 연습 - 표 편집 | 프로그래머스 (programmers.co.kr)
코딩테스트 연습 - 표 편집
8 2 ["D 2","C","U 3","C","D 4","C","U 2","Z","Z"] "OOOOXOOO" 8 2 ["D 2","C","U 3","C","D 4","C","U 2","Z","Z","U 1","C"] "OOXOXOOO"
programmers.co.kr
이중 연결 리스트 구현 문제이다.
이 문제를 처음 접했을 때 union find 를 이용하여 삭제된 표들을 grouping 을 통해 U, D operation 을 최소화하려고 했으나 Z operation 이 문제였다.
그래서 현재 가르키고 있는 위치에서 Delete 를 O(1) 에 할 수 있는 방법을 생각하다가 연결 리스트를 떠올렸다.
우선 ArrayList 와 LinkedList 에 대해서 delete 에 대한 시간 복잡도를 고려할 필요가 있다.
- ArrayList : 최악의 경우 첫 번째 원소를 제거한다고 할 때 나머지 원소들을 하나씩 아래로 내리는 작업을 하는데 드는 비용이 O(n) 이 된다.
- LinkedList : 현재 노드를 제거하는데 next, prev 만 건드리면 되므로 O(1) 이 된다.
delete 는 확실하게 해결한 것 같다.
그러나 연결 리스트를 통해서 U, D operation 을 하려고 할 때 인덱스를 통해 접근할 수 없어서 최악의 경우 매번 O(n) 만큼 이동해야 하는데 이를 해결할 수 있는지 의문이 들었다.
하지만 이러한 고민은 쓸데없는 고민이였다.
cmd에 등장하는 모든 X들의 값을 합친 결과가 1,000,000 이하인 경우만 입력으로 주어집니다.
그렇다.
모든 X 값들을 합한게 1,000,000 이하면 결국 연결리스트를 next, prev 를 통해 노드를 이동하는 operation 을 자유롭게 할 수 있다.
operation 을 처리하기 전에 표 들을 어떻게 연결리스트로 나타낼 지, 그리고 삭제된 표 들을 어떻게 보관할지에 대해서 살펴보도록 하자.
typedef struct node {
struct node* prev;
struct node* next;
int num;
} Node;
Node* head, * pos;
Node* Stack[1000001];
Node dummy[1000001];
int top;
노드들을 위 아래로 이동할 수 있도록 prev, next 를 선언하였다.
그리고 해당 표의 행의 번호를 식별할 수 있도록 num 을 선언하였다.
head 는 표 들의 정보를 담도록 하였고 pos 는 현재 가르키고 있는 표를 담도록 하였다.
Stack 은 삭제된 표 들을 담도록 하여 가장 마지막에 삭제된 표가 가장 먼저 복원되도록 선언하였다.
dummy 배열은 malloc 대신 전역 변수로 선언한 dummy 의 원소들을 head 가 가르키도록 하기 위함이다.
top 은 현재 삭제된 표의 갯수이다.
이번엔 n, k 값을 통해 연결 리스트의 노드를 세팅하도록 하는 함수를 보자.
void set_node(int n, int k) {
Node* tmp;
head = &dummy[1000000];
tmp = head;
for (int i = 0; i < n; i++) {
dummy[i].num = i;
tmp->next = &dummy[i];
tmp->next->prev = tmp;
tmp = tmp->next;
}
tmp = head;
for (int i = 0; i <= k; i++) {
tmp = tmp->next;
}
pos = tmp;
}
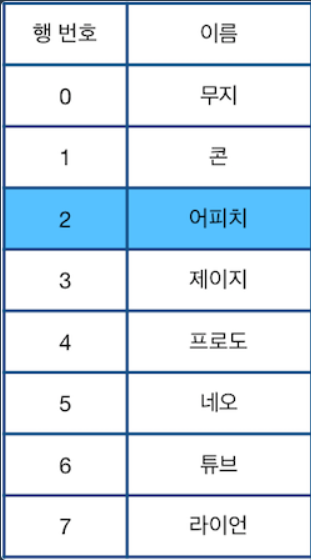
위 표는 n = 8, k = 2 인 경우다.
이를 위 코드를 통해 연결 리스트로 나타내면 다음과 같다.

그러면 operation 별로 어떻게 처리해야 할 지에 대해서 살펴보도록 하자.
① "U X" : 행의 번호를 X 번 만큼 위로 올려야 한다.
위로 올린다는 것은 행 번호가 감소되는 것을 의미한다.
즉, 현재 위치에서 prev 으로 X 번 만큼 이동하면 된다.
void go_up(int X) {
// prev
while (X--) {
pos = pos->prev;
}
}
② "D X" : 행의 번호를 X 번 만큼 아래로 내려야 한다.
아래로 내린다는 것은 행 번호가 증가하는 것을 의미한다.
즉, 현재 위치에서 next 으로 X 번 만큼 이동하면 된다.
void go_down(int X) {
// next
while (X--) {
pos = pos->next;
}
}
③ "C" : 현재 가르키고 있던 위치의 표를 제거한다.
그리고 현재 가르키고 있던 위치의 다음 위치를 현재 가르키고 있는 위치로 변경한다.
2 가지 케이스를 고려할 수 있다.
(1) 가장 마지막을 제외한 나머지를 가르키고 있는 표
pos 를 기준으로 하여 prev 에 위치한 표를 pos 를 기준으로 하여 next 에 위치한 표를 가르키도록 해야 한다.
pos 를 기준으로 하여 next 에 위치한 표를 pos 를 기준으로 하여 prev 에 위치한 표를 가르키도록 해야 한다.
그리고 현재 가르키고 있는 pos 를 Stack 에 담고 pos 를 pos 의 next 에 위치한 표를 가르키도록 변경한다.

위와 같은 상태에서 행 번호가 2인 표를 제거하여 스택에 담는 작업을 한다.
pos->prev->next = pos->next;
위 코드를 수행하면 다음과 같다.

pos->next->prev = pos->prev;
위 코드를 수행하면 다음과 같다.

이제 행 번호가 2인 표를 스택에 담아야 한다.
stack[top++] = pos;
위 코드를 수행하면 다음과 같다.

그리고 현재 가르키고 있는 pos 를 pos->next 를 가르키도록 해야 한다.
pos = pos->next;
위 코드를 수행하면 다음과 같다.

(2) 가장 마지막을 가르키고 있는 표
pos 를 기준으로 하여 prev 에 위치한 표를 pos 를 기준으로 하여 next 에 위치한 표를 가르키도록 해야 한다.
그리고 현재 가르키고 있는 pos 를 Stack 에 담고 pos 를 pos 의 prev 에 위치한 표를 가르키도록 변경한다.
(1), (2) 를 코드로 나타내면 다음과 같다.
void go_delete() {
if (pos->next) {
pos->prev->next = pos->next;
pos->next->prev = pos->prev;
}
else {
pos->prev->next = 0;
}
Stack[top++] = pos;
if (pos->next) pos = pos->next;
else pos = pos->prev;
}
④ "Z" : 가장 최근에 삭제한 표를 복구한다.
이를 해결하기 위해서 Stack 의 (top - 1) 에 가르키고 있는 표를 head 에 있는 표들 사이에 연결시켜야 한다.
Stack 의 (top - 1) 에 가르키고 있는 표를 tmp 라고 할 때, tmp 의 next 가 있을 경우와 없는 경우를 나눌 수 있다.
(1) tmp 의 next 가 있을 경우
다음과 같은 상황에서 표들을 연결해야 한다고 해보자.

우선 행 번호가 1인 표를 행 번호가 2 인 표를 가르키도록 해야 한다.
tmp->prev->next = tmp;
위 코드를 수행하면 다음과 같다.
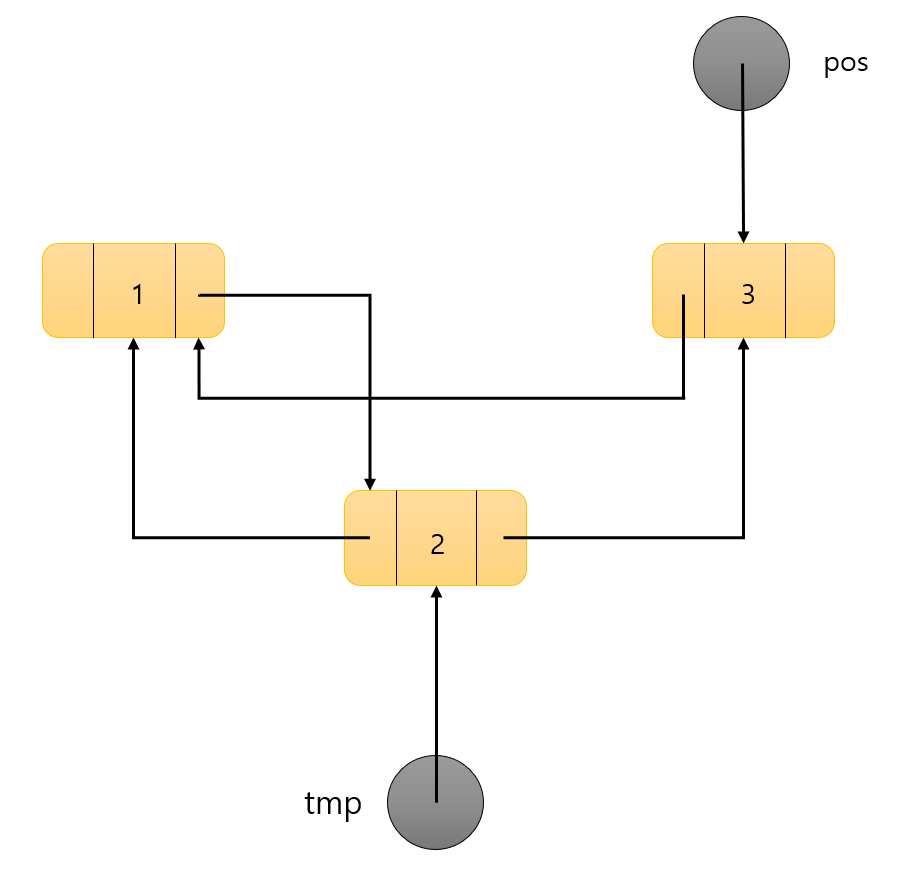
그리고 행 번호가 3인 표를 행 번호가 2인 표를 가르키도록 해야 한다.
tmp->next->prev = tmp;
위 코드를 수행하며 다음과 같다.

(2) tmp 의 next 가 없을 경우
이 경우는 tmp->prev->next = tmp 만 수행하면 된다. (tmp->next 는 NULL 이기 때문)
(1), (2) 를 코드로 나타내면 다음과 같다.
void go_update() {
Node* tmp;
tmp = Stack[--top];
if (tmp->next) {
tmp->prev->next = tmp;
tmp->next->prev = tmp;
}
else {
tmp->prev->next = tmp;
}
}
위와 같이 모든 operation 을 다 수행했다고 해보자.
그러면 head 에 남아있는 행 번호들을 수확해서 수확한 행 번호들을 'O', 수확하지 못한 행 번호들을 'X' 으로 문자열을 형성하면 된다.
이에 대한 코드는 다음과 같다.
for (Node* tmp = head->next; tmp != 0; tmp = tmp->next) {
visited[tmp->num] = true;
}
for (int i = 0; i < n; i++) {
if (visited[i]) answer += 'O';
else answer += 'X';
}
문제 풀이 코드
#include <string>
#include <vector>
using namespace std;
typedef struct node {
struct node* prev;
struct node* next;
int num;
} Node;
Node* head, * pos;
Node* Stack[1000001];
Node dummy[1000001];
int top;
bool visited[1000001];
void set_node(int n, int k) {
Node* tmp;
head = &dummy[1000000];
tmp = head;
for (int i = 0; i < n; i++) {
dummy[i].num = i;
tmp->next = &dummy[i];
tmp->next->prev = tmp;
tmp = tmp->next;
}
tmp = head;
for (int i = 0; i <= k; i++) {
tmp = tmp->next;
}
pos = tmp;
}
void go_up(int X) {
// prev
while (X--) {
pos = pos->prev;
}
}
void go_down(int X) {
// next
while (X--) {
pos = pos->next;
}
}
void go_delete() {
if (pos->next) {
pos->prev->next = pos->next;
pos->next->prev = pos->prev;
}
else {
pos->prev->next = 0;
}
Stack[top++] = pos;
if (pos->next) pos = pos->next;
else pos = pos->prev;
}
void go_update() {
Node* tmp;
tmp = Stack[--top];
if (tmp->next) {
tmp->prev->next = tmp;
tmp->next->prev = tmp;
}
else {
tmp->prev->next = tmp;
}
}
string solution(int n, int k, vector<string> cmd) {
string answer = "";
int X;
set_node(n, k);
for (int i = 0; i < cmd.size(); i++) {
if (cmd[i][0] == 'U') {
X = stoi(&cmd[i][2]);
go_up(X);
}
else if (cmd[i][0] == 'D') {
X = stoi(&cmd[i][2]);
go_down(X);
}
else if (cmd[i][0] == 'C') {
go_delete();
}
else if (cmd[i][0] == 'Z') {
go_update();
}
}
for (Node* tmp = head->next; tmp != 0; tmp = tmp->next) {
visited[tmp->num] = true;
}
for (int i = 0; i < n; i++) {
if (visited[i]) answer += 'O';
else answer += 'X';
}
return answer;
}
4. 미로 탈출
문제 링크 : 코딩테스트 연습 - 미로 탈출 | 프로그래머스 (programmers.co.kr)
코딩테스트 연습 - 미로 탈출
4 1 4 [[1, 2, 1], [3, 2, 1], [2, 4, 1]] [2, 3] 4
programmers.co.kr
비트마스킹을 이용한 다익스트라 문제이다.
이 문제는 처음에 문제를 정확하게 파악하지 못해서 30% 에 도달하였다.
놓쳤던 부분은 다음과 같다.
1. trap 에 도착하면 인접한 방에 대한 간선 방향을 뒤집어야 한다.
인접한 방이 아니라 모든 방에 대한 간선 방향을 뒤집어야 한다고 생각해서 틀렸다.
이를 수정하니 전체 케이스 중 2 케이스만 틀리게 되었다.
2. dist > D[cur][trap_bit] 에 대한 조건문을 trap_bit 을 update 전에 처리해야 한다.
다익스트라를 처리할 때, 무한 루프를 방지하기 위해 위와 같은 조건을 설정하는데 trap_bit 을 update 한 후에 처리를 해서 틀린 것이었다.
뜬금없이 trap_bit 가 나타났는데 문제를 설명하면서 자연스럽게 설명하도록 하겠다.
※ 문제 접근 순서
① trap 이 발동되지 않은 경우와 발동된 경우의 간선 정보를 담는다.
vector<pair<int, int>> v[1001][2];
위 벡터를 통해서 간선 정보를 담도록 했다.
예를 들어 from 에서 to 로 dist 만큼 걸린다고 할 때
- v[from][0] = { {to, dist} } : trap 이 발동되지 않은 경우 0 으로 설정하여 간선 정보를 push 했다.
- v[to][1] = { {from, dist} } : trap 이 발동된 경우 1 으로 설정하여 간선 정보를 push 했다.
② 비트마스킹을 하기 위해 trap 방에 대한 Trap 배열에 대해 초기화 작업을 진행한다.
int Trap[1001];
for (int i = 0; i < traps.size(); i++) {
Trap[traps[i]] = 1 << i;
}
미리 \(2^{i}\) 를 해당 trap 방에 할당하여 좀 더 편리하게 연산하기 위해 위와 같이 구현하였다.
문제에서 trap 방은 최대 10 개라고 했으므로 최대 10 bit 를 활용하여 어떤 방이 trap 이 발동된 건지 아닌지를 판단할 수 있다.
예를 들어서 trap 방이 5 개라고 가정해보자.
초기 상태는 [0, 0, 0, 0, 0] 으로 한 번도 trap 방에 방문하지 않은 경우로 볼 수 있다.
그렇다면 3 번째 trap 방과 5 번째 trap 방에 방문한 경우는 [0, 0, 1, 0, 1] 으로 bitmask 를 통해 확인할 수 있다.
즉, trap 방이 n 개일 경우 \(2^{n}\) 가지의 경우를 고려하여 다익스트라 알고리즘을 활용해야 하는 것을 유추할 수 있다.
③ 다익스트라 알고리즘을 활용한다.
단순히 다익스트라 알고리즘을 활용하기엔 뭔가 정리가 안된 것 같다.
문제에서 trap 방에 방문하면 trap 방의 인접한 간선의 방향이 거꾸로 변경되는 것을 언급했는데 이에 대한 케이스를 분류해 볼 필요가 있다.
다음과 같은 그래프가 있다고 가정하자.

(1) 현재 정점이 trap 이 발동되지 않고 다음 정점이 trap 이 발동되지 않은 경우
이 경우는 trap 이 발동되지 않은 간선 정보를 활용하여 이동하면 된다.
즉, 벡터 v 의 인덱스 0 을 통해 간선 정보를 활용하며 1 번 정점에서 2 번 정점으로 이동하는 경우로 볼 수 있다.
(2) 현재 정점이 trap 이 발동되고 다음 정점이 trap 이 발동되지 않은 경우
이 경우는 trap 이 발동된 간선 정보를 활용하여 이동해야 한다.
우선 1 번 정점에서 2 번 정점으로 이동한 경우 trap 방에 이동하게 된 경우이므로 trap 방에 인접한 간선의 방향을 거꾸로 변경시키고 bitmask 를 수행해야 한다.

위 사진과 같이 간선 방향을 변경시키고 bitmask 를 통해 2 번 trap 방이 trap 이 발동된 것을 나타내야 한다.
벡터 v 의 인덱스 1을 통해 간선 정보를 활용하며 2 번 정점에서 1 번 정점 또는 3 번 정점으로 이동하는 경우로 볼 수 있다.
(3) 현재 정점이 trap 이 발동되지 않고 다음 정점이 trap 이 발동된 경우
이 경우는 trap 이 발동된 간선 정보를 활용하여 이동해야 한다.
2 번 정점에서 1 번 정점으로 다시 돌아와서 1 번 정점에서 trap 방인 2 번 정점으로 이동하는 경우를 고려해보자.

간선이 현재 trap 이 발동되지 않은 간선 정보가 아닌 trap 이 발동된 간선 정보임을 알 수 있다.
즉, 벡터 v 의 인덱스 1을 통해 간선 정보를 활용하며 1 번 정점에서 2 번 정점으로 이동하는 경우로 볼 수 있다.
(4) 현재 정점이 trap 이 발동되고 다음 정점이 trap 이 발동된 경우
이 경우는 trap 이 발동되지 않은 간선 정보를 활용해야 한다.
1 번 정점에서 2 번 정점으로 이동하고 trap 이 발동된 후에 2 번 정점에서 3 번 정점으로 이동한 경우를 고려해보자.
우선 3 번 정점으로 도착하면 trap 방이므로 trap 이 발동되어야 한다.
그러면 다음과 같이 그래프가 변경된다.

간선이 현재 trap 이 발동되지 않은 간선 정보임을 알 수 있다.
즉, 벡터 v 의 인덱스 0을 통해 간선 정보를 활용하며 3 번 정점에서 2 번 정점으로 이동하는 경우로 볼 수 있다.
여기서 좀 더 다르게 생각해보자.
만약 trap 이 발동되지 않은 간선 정보가 3 번에서 4 번을 가르키는 방향이 아닌 4 번에서 3 번을 가르키는 방향이라고 가정해보자.
그리고 1 번 정점에서 2 번 정점으로 이동하고 trap 이 발동된 후에 3 번 정점으로 이동한 경우를 고려해보자.

3 번 정점에 도착하게 되면 trap 방이므로 trap 이 발동하게 된다.
trap 이 발동되면 다음과 같이 그래프가 변경된다.

우선 (4) 조건에 의하면 3 번 정점에서 2 번 정점으로 이동이 가능하다.
그렇다면 3 번 정점에서 4 번 정점으로 이동하는 경우는 어떤 조건에 의한건가?
(2) 조건으로 현재 정점이 trap 이 발동되고 다음 정점이 trap 이 발동되지 않은 경우에 의해 trap 이 발동된 간선 정보를 통해 이동이 가능하게 된 것이다.
이제 틀이 잡힌 것 같다.
그러면 코드를 살펴보도록 한다.
void dijkstra(int n, int start) {
priority_queue<pair<pair<int, int>, int>> PQ;
// { { distance, node }, trap_bit } }
// trap_bit = 0 0 0 0 0 0 0 0 0 0
for (int i = 1; i <= n; i++) {
for (int j = 0; j < 1024; j++) {
D[i][j] = 1e9;
}
}
PQ.push({ {0, start}, 0 });
D[start][0] = 0;
...
}
j 의 범위를 잘 보자.
0 부터 1023 까지 모든 정점들에 도달할 수 있는 거리를 1e9 로 할당해줬는데 trap 방이 최대 10개 존재한다.
즉, trap 이 발동된 경우, 발동되지 않은 경우에 대한 모든 경우가 1024 가지이기 때문이다.
그리고 우선순위 큐 PQ 를 선언하여 { distance, node, trap_bit } 을 할당해줬다.
여기서 trap_bit 은 trap 방들이 trap 이 발동되었는지 발동되지 않았는지에 대한 bitmask 역할을 한다.
그 이후의 코드를 살펴보도록 한다.
...
while (!PQ.empty()) {
int dist = -PQ.top().first.first, cur = PQ.top().first.second;
int trap_bit = PQ.top().second;
PQ.pop();
if (dist > D[cur][trap_bit])
continue;
if (Trap[cur]) {
if (trap_bit & Trap[cur]) trap_bit -= Trap[cur];
else trap_bit += Trap[cur];
}
for (pair<int, int> p : v[cur][0]) {
int next = p.first, next_dist = dist + p.second;
if (((trap_bit & Trap[cur]) && (trap_bit & Trap[next]))
|| (!(trap_bit & Trap[cur]) && !(trap_bit & Trap[next]))) {
if (next_dist < D[next][trap_bit]) {
D[next][trap_bit] = next_dist;
PQ.push({ {-next_dist, next}, trap_bit });
}
}
}
for (pair<int, int> p : v[cur][1]) {
int next = p.first, next_dist = dist + p.second;
if (((trap_bit & Trap[cur]) && !(trap_bit & Trap[next]))
|| (!(trap_bit & Trap[cur]) && (trap_bit & Trap[next]))) {
if (next_dist < D[next][trap_bit]) {
D[next][trap_bit] = next_dist;
PQ.push({ {-next_dist, next}, trap_bit });
}
}
}
}
}
여기서 if (dist > D[cur][trap_bit]) 에 대한 조건문의 위치를 조심해야 한다.
만약 trap_bit 을 update 한 후에 조건문을 둔다면 틀린다.
즉, 방문했던 정점을 또 다시 방문하게 된 경우 D[cur][trap_bit] 값이 이미 update 될 수 있다는 것을 암시하는데 이 경우 dist 는 또 다시 방문하게 된 경우이므로 확실하게 D[cur][trap_bit] 값보다 크다.
이러한 상황을 방지하기 위해 trap_bit 을 update 하기 전에 조건문을 달아야 한다.
그 후에 v 의 index 를 0, 1 으로 두 가지 경우로 나눠서 trap 이 발동되지 않은 간선과 발동된 간선을 위에서 언급한 조건을 활용하여 이동시키면 된다.
다익스트라 알고리즘의 시간 복잡도는 간선의 갯수가 E, 정점의 갯수를 V 라고 할 때 \(O(E \times logV)\) 이다.
근데 bitmask 를 통해 \(0(0000000000_{2})\) 부터 \(1023(1111111111_{2})\) 까지 총 1024 가지를
고려해야 하므로 \(O(1024 \times E \times logV)\) 이다.
문제 풀이 코드
#include <string>
#include <vector>
#include <queue>
using namespace std;
vector<pair<int, int>> v[1001][2];
int D[1001][1024];
int Trap[1001];
void dijkstra(int n, int start) {
priority_queue<pair<pair<int, int>, int>> PQ;
// { { distance, node }, trap_bit } }
// trap_bit = 0 0 0 0 0 0 0 0 0 0
for (int i = 1; i <= n; i++) {
for (int j = 0; j < 1024; j++) {
D[i][j] = 1e9;
}
}
PQ.push({ {0, start}, 0 });
D[start][0] = 0;
while (!PQ.empty()) {
int dist = -PQ.top().first.first, cur = PQ.top().first.second;
int trap_bit = PQ.top().second;
PQ.pop();
if (dist > D[cur][trap_bit])
continue;
if (Trap[cur]) {
if (trap_bit & Trap[cur]) trap_bit -= Trap[cur];
else trap_bit += Trap[cur];
}
for (pair<int, int> p : v[cur][0]) {
int next = p.first, next_dist = dist + p.second;
if (((trap_bit & Trap[cur]) && (trap_bit & Trap[next]))
|| (!(trap_bit & Trap[cur]) && !(trap_bit & Trap[next]))) {
if (next_dist < D[next][trap_bit]) {
D[next][trap_bit] = next_dist;
PQ.push({ {-next_dist, next}, trap_bit });
}
}
}
for (pair<int, int> p : v[cur][1]) {
int next = p.first, next_dist = dist + p.second;
if (((trap_bit & Trap[cur]) && !(trap_bit & Trap[next]))
|| (!(trap_bit & Trap[cur]) && (trap_bit & Trap[next]))) {
if (next_dist < D[next][trap_bit]) {
D[next][trap_bit] = next_dist;
PQ.push({ {-next_dist, next}, trap_bit });
}
}
}
}
}
int solution(int n, int start, int end, vector<vector<int>> roads, vector<int> traps) {
int answer = 1e9;
for (int i = 0; i < roads.size(); i++) {
int from = roads[i][0], to = roads[i][1];
int dist = roads[i][2];
v[from][0].push_back({ to, dist });
v[to][1].push_back({ from,dist });
}
for (int i = 0; i < traps.size(); i++) {
Trap[traps[i]] = 1 << i;
}
dijkstra(n, start);
for (int i = 0; i < 1024; i++) {
answer = min(answer, D[end][i]);
}
return answer;
}
'프로그래머스' 카테고리의 다른 글
| 2023 KAKAO BLIND RECRUITMENT 문제 리뷰 (7) | 2023.01.12 |
|---|---|
| 2021 KAKAO BLIND RECRUITMENT 문제 리뷰 (0) | 2022.03.01 |
| 2022 KAKAO BLIND RECRUITMENT 문제 리뷰 (0) | 2022.01.22 |



