mojo's Blog
[백준 6549] 히스토그램에서 가장 큰 직사각형 본문
문제 링크 : 6549번: 히스토그램에서 가장 큰 직사각형 (acmicpc.net)
6549번: 히스토그램에서 가장 큰 직사각형
입력은 테스트 케이스 여러 개로 이루어져 있다. 각 테스트 케이스는 한 줄로 이루어져 있고, 직사각형의 수 n이 가장 처음으로 주어진다. (1 ≤ n ≤ 100,000) 그 다음 n개의 정수 h1, ..., hn (0 ≤ hi ≤
www.acmicpc.net
문제
히스토그램은 직사각형 여러 개가 아래쪽으로 정렬되어 있는 도형이다. 각 직사각형은 같은 너비를 가지고 있지만, 높이는 서로 다를 수도 있다. 예를 들어, 왼쪽 그림은 높이가 2, 1, 4, 5, 1, 3, 3이고 너비가 1인 직사각형으로 이루어진 히스토그램이다.
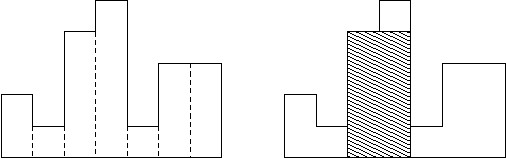
히스토그램에서 가장 넓이가 큰 직사각형을 구하는 프로그램을 작성하시오.
입력
입력은 테스트 케이스 여러 개로 이루어져 있다. 각 테스트 케이스는 한 줄로 이루어져 있고, 직사각형의 수 n이 가장 처음으로 주어진다. (1 ≤ n ≤ 100,000) 그 다음 n개의 정수 h1, ..., hn (0 ≤ hi ≤ 1,000,000,000)가 주어진다. 이 숫자들은 히스토그램에 있는 직사각형의 높이이며, 왼쪽부터 오른쪽까지 순서대로 주어진다. 모든 직사각형의 너비는 1이고, 입력의 마지막 줄에는 0이 하나 주어진다.
출력
각 테스트 케이스에 대해서, 히스토그램에서 가장 넓이가 큰 직사각형의 넓이를 출력한다.
세그먼트 트리 문제이다.
사실 스택 풀이법이 존재하지만 어제 공부했던 세그먼트 트리를 활용하고 싶어서 세그먼트 트리 풀이법으로 접근하였다.
※ 문제 아이디어
1. 히스토그램에서 가장 높이가 작은 직사각형의 인덱스를 구한다.
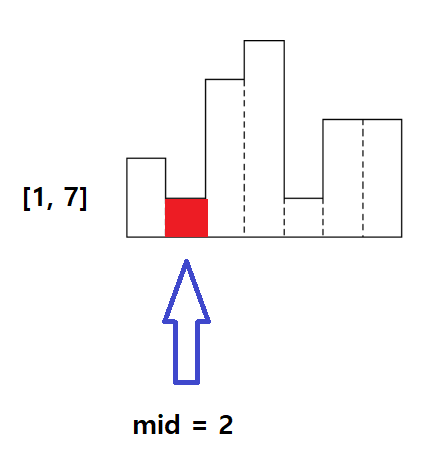
2. [left, right] 범위에서 가장 높이가 작은 직사각형에 대해서 넓이를 구한다.
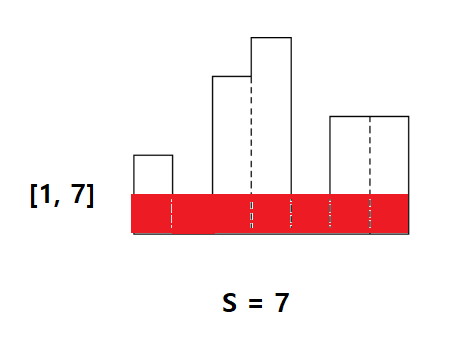
3. 1번에서 구한 인덱스를 기준으로 [left, mid - 1], [mid + 1, right] 으로 히스토그램을 분리한다.

4. 나뉘어진 두 히스토그램 각각 1번 방법을 수행함으로써 재귀적인 진행이 이뤄지도록 한다.
이때 [left, right] 범위에서 left > right 인 케이스일 경우 따로 처리해줘야 한다.
※ 문제 접근 방법
1. [left, right] 범위에서의 세그트리의 값을 해당 범위 내에서 가장 높이가 작은 직사각형의 인덱스라고 정의한다.
그렇다면 세그트리를 다음과 같이 설정할 수 있다.
void set_Segtree(int idx, int left, int right) {
if (left == right) {
segTree[idx] = left;
return;
}
int mid = (left + right) / 2;
set_Segtree(2 * idx, left, mid);
set_Segtree(2 * idx + 1, mid + 1, right);
segTree[idx] = X[segTree[2 * idx]] > X[segTree[2 * idx + 1]] ? segTree[2 * idx + 1] : segTree[2 * idx];
}
2. [left, right] 범위에서 가장 높이가 작은 직사각형의 인덱스를 구한다.
인덱스를 구하는 방법은 다음과 같다.
int query_Segtree(int idx, int left, int right, int q_left, int q_right) {
if (right < q_left || q_right < left) return -1;
if (q_left <= left && right <= q_right) {
return segTree[idx];
}
int mid = (left + right) / 2;
int A = query_Segtree(2 * idx, left, mid, q_left, q_right);
int B = query_Segtree(2 * idx + 1, mid + 1, right, q_left, q_right);
if (A == -1) return B;
if (B == -1) return A;
if (X[A] > X[B]) return B;
return A;
}- 둘 중 하나는 범위에 포함하지 않는 경우가 존재한다. 따라서 둘 중 하나의 값이 -1일 경우 다른 인덱스 값을 반환하면 된다.
- X[A] > X[B] : A 인덱스의 직사각형 높이보다 B 인덱스의 직사각형 높이가 작다면 인덱스 B를 리턴하고 그렇지 않은 경우 A를 반환하면 된다.
3. 2번에서 얻은 인덱스를 mid라고 한다면 [left, right] 범위에서의 직사각형 넓이를 다음과 같이 구할 수 있다.
int mid = query_Segtree(1, 1, n, left, right);
ll S = (ll)(right - left + 1) * X[mid];
4. [left, mid - 1], [right, mid + 1] 범위 각각 재귀적으로 위 과정을 수행시켜야 한다.
다음과 같이 재귀적으로 답을 구할 수 있다.
ll max_Square(int left, int right) {
if (left == right) {
return X[left];
}
int mid = query_Segtree(1, 1, n, left, right);
ll S = (ll)(right - left + 1) * X[mid];
if (left <= mid - 1) {
S = max(S, max_Square(left, mid - 1));
}
if (mid + 1 <= right) {
S = max(S, max_Square(mid + 1, right));
}
return S;
}- 초기 호출은 max_Square(1, n) 이며, 호출값은 [1, n] 범위내에서의 히스토그램에서 가장 큰 직사각형의 넓이가 된다.
Solution Code
#define _CRT_SECURE_NO_WARNINGS
#include <string>
#include <stdio.h>
#include <math.h>
#include <iostream>
#include <vector>
#include <algorithm>
#include <map>
#include <queue>
#include <stack>
#include <time.h>
#define INF 1000000000
#define endl '\n'
#define ll long long
using namespace std;
int n;
ll X[100001];
int segTree[300001];
bool input() {
cin >> n;
if (n == 0) return false;
for (int i = 1; i <= n; i++) {
cin >> X[i];
}
return true;
}
void set_Segtree(int idx, int left, int right) {
if (left == right) {
segTree[idx] = left;
return;
}
int mid = (left + right) / 2;
set_Segtree(2 * idx, left, mid);
set_Segtree(2 * idx + 1, mid + 1, right);
segTree[idx] = X[segTree[2 * idx]] > X[segTree[2 * idx + 1]] ? segTree[2 * idx + 1] : segTree[2 * idx];
}
int query_Segtree(int idx, int left, int right, int q_left, int q_right) {
if (right < q_left || q_right < left) return -1;
if (q_left <= left && right <= q_right) {
return segTree[idx];
}
int mid = (left + right) / 2;
int A = query_Segtree(2 * idx, left, mid, q_left, q_right);
int B = query_Segtree(2 * idx + 1, mid + 1, right, q_left, q_right);
if (A == -1) return B;
if (B == -1) return A;
if (X[A] > X[B]) return B;
return A;
}
ll max_Square(int left, int right) {
if (left == right) {
return X[left];
}
int mid = query_Segtree(1, 1, n, left, right);
ll S = (ll)(right - left + 1) * X[mid];
if (left <= mid - 1) {
S = max(S, max_Square(left, mid - 1));
}
if (mid + 1 <= right) {
S = max(S, max_Square(mid + 1, right));
}
return S;
}
void solution() {
set_Segtree(1, 1, n);
cout << max_Square(1, n) << endl;
}
int main()
{
ios_base::sync_with_stdio(false); cin.tie(0); cout.tie(0);
while (input()) {
solution();
}
return 0;
}

'백준 > Tree' 카테고리의 다른 글
| [백준 11812] K진 트리 (0) | 2022.01.24 |
|---|---|
| [백준 14725] 개미굴 (0) | 2021.12.26 |
| [백준 2250] 트리의 높이와 너비 (0) | 2021.12.24 |
| [백준 2042] 구간 합 구하기 (0) | 2021.07.29 |




