mojo's Blog
[백준 15685] 드래곤 커브 본문
문제 링크 => 15685번: 드래곤 커브 (acmicpc.net)
15685번: 드래곤 커브
첫째 줄에 드래곤 커브의 개수 N(1 ≤ N ≤ 20)이 주어진다. 둘째 줄부터 N개의 줄에는 드래곤 커브의 정보가 주어진다. 드래곤 커브의 정보는 네 정수 x, y, d, g로 이루어져 있다. x와 y는 드래곤 커
www.acmicpc.net
문제
드래곤 커브는 다음과 같은 세 가지 속성으로 이루어져 있으며, 이차원 좌표 평면 위에서 정의된다. 좌표 평면의 x축은 → 방향, y축은 ↓ 방향이다.
- 시작 점
- 시작 방향
- 세대
0세대 드래곤 커브는 아래 그림과 같은 길이가 1인 선분이다. 아래 그림은 (0, 0)에서 시작하고, 시작 방향은 오른쪽인 0세대 드래곤 커브이다.

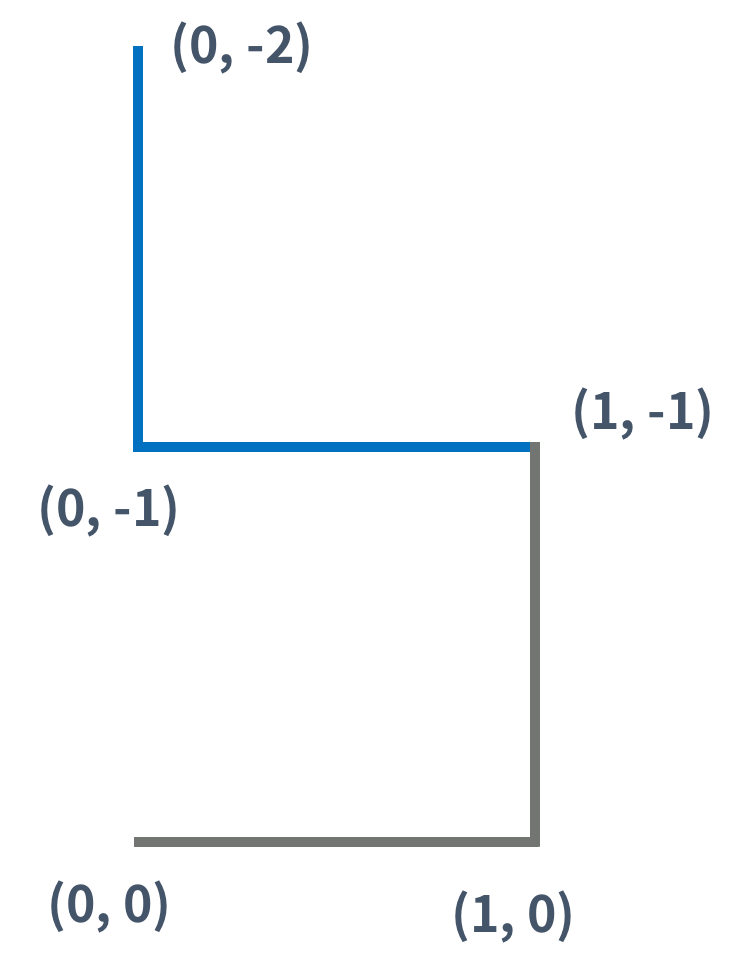
1세대 드래곤 커브는 0세대 드래곤 커브를 끝 점을 기준으로 시계 방향으로 90도 회전시킨 다음 0세대 드래곤 커브의 끝 점에 붙인 것이다. 끝 점이란 시작 점에서 선분을 타고 이동했을 때, 가장 먼 거리에 있는 점을 의미한다.

2세대 드래곤 커브도 1세대를 만든 방법을 이용해서 만들 수 있다. (파란색 선분은 새로 추가된 선분을 나타낸다)
3세대 드래곤 커브도 2세대 드래곤 커브를 이용해 만들 수 있다. 아래 그림은 3세대 드래곤 커브이다.
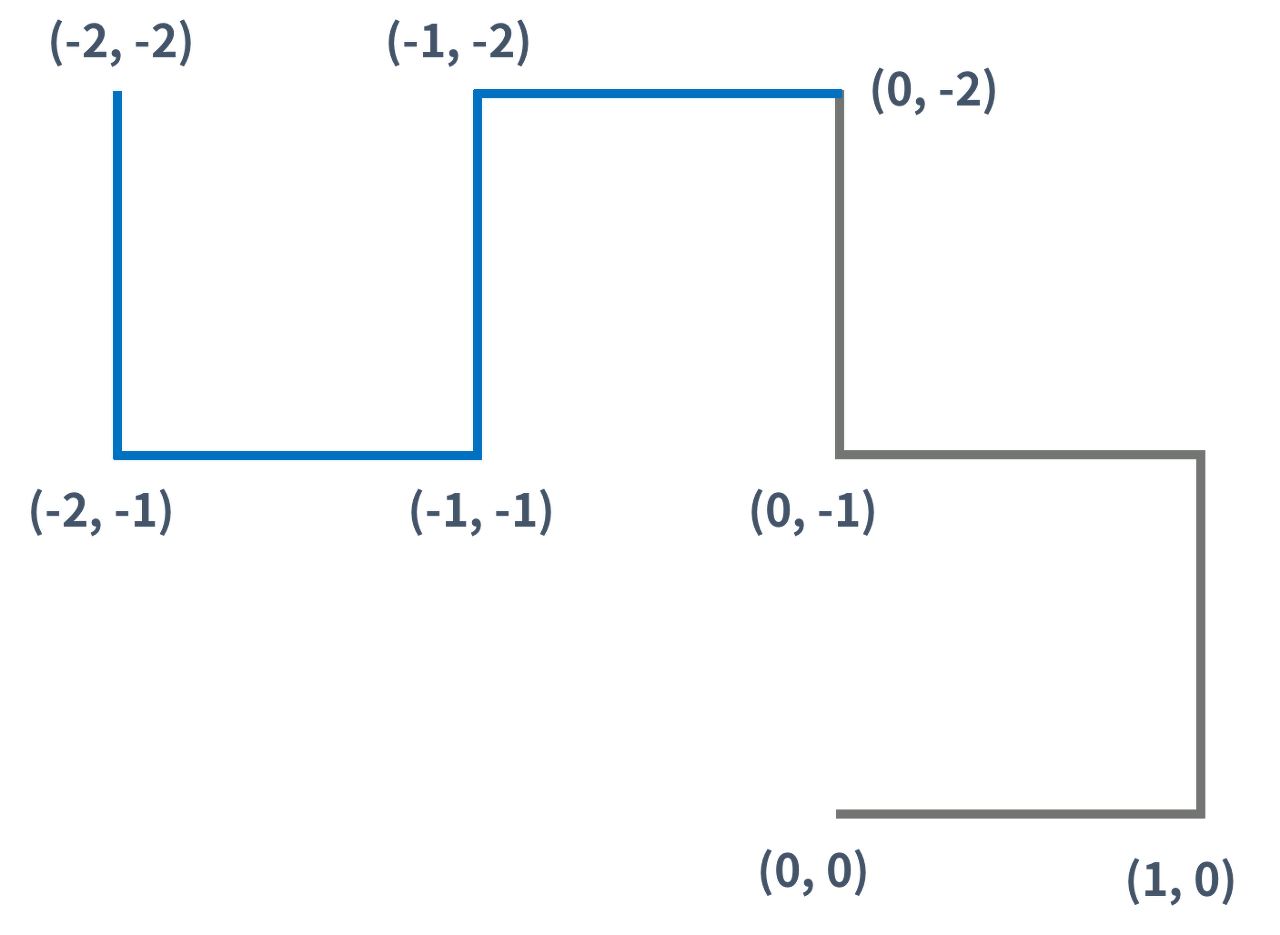
즉, K(K > 1)세대 드래곤 커브는 K-1세대 드래곤 커브를 끝 점을 기준으로 90도 시계 방향 회전 시킨 다음, 그것을 끝 점에 붙인 것이다.
크기가 100×100인 격자 위에 드래곤 커브가 N개 있다. 이때, 크기가 1×1인 정사각형의 네 꼭짓점이 모두 드래곤 커브의 일부인 정사각형의 개수를 구하는 프로그램을 작성하시오. 격자의 좌표는 (x, y)로 나타내며, 0 ≤ x ≤ 100, 0 ≤ y ≤ 100만 유효한 좌표이다.
입력
첫째 줄에 드래곤 커브의 개수 N(1 ≤ N ≤ 20)이 주어진다. 둘째 줄부터 N개의 줄에는 드래곤 커브의 정보가 주어진다. 드래곤 커브의 정보는 네 정수 x, y, d, g로 이루어져 있다. x와 y는 드래곤 커브의 시작 점, d는 시작 방향, g는 세대이다. (0 ≤ x, y ≤ 100, 0 ≤ d ≤ 3, 0 ≤ g ≤ 10)
입력으로 주어지는 드래곤 커브는 격자 밖으로 벗어나지 않는다. 드래곤 커브는 서로 겹칠 수 있다.
방향은 0, 1, 2, 3 중 하나이고, 다음을 의미한다.
- 0: x좌표가 증가하는 방향 (→)
- 1: y좌표가 감소하는 방향 (↑)
- 2: x좌표가 감소하는 방향 (←)
- 3: y좌표가 증가하는 방향 (↓)
출력
첫째 줄에 크기가 1×1인 정사각형의 네 꼭짓점이 모두 드래곤 커브의 일부인 것의 개수를 출력한다.
구현 및 시뮬레이션 문제이다.
접근 방법은 다음과 같다.
1. input으로 x, y, d, g를 받으면 0세대 드래곤 커브를 형성한다. (방향 d를 이용하여 선분 형성)
2. g가 0이면 드래곤 커브가 완성이며 1 이상일 경우 끝 점을 기준으로 시계 방향으로 90도 회전을 하여 완성시킨다.
3. 100x100 격자 위에 드래곤 커브의 점들을 표시한다.
4. 1 ~ 3 의 작업이 모두 끝나면, 격자 위에 표시된 정점들을 살피면서 1x1 정사각형의 갯수를 카운팅한다.
1번 방법은 d를 기준으로 선분을 형성해주면 끝이다.
2번 방법은 g 세대 드래곤 커브를 형성하기 위해 (g - 1) 세대 드래곤 커브의 끝 점을 기준으로 나머지 점들을 시계 방향으로 90도 회전을 하여 (g - 1) 세대 드래곤 커브에 점들을 추가해줘야 한다.
끝 지점을 센터 점 (a, b) 로 잡고 90도로 회전시키고자 할 임의의 점을 (x, y) 라고 할 때, 다음과 같이 회전이 가능하다.

편의상 보기 편하게 위와 같이 2차원 평면에 배치한다면 반시계 방향으로 90도 회전을 하는것으로 알 수 있다.
(1) 센터 점 (a, b) 에서 임의의 점 (x, y) 으로의 방향 벡터 \(\overrightarrow{d}\) 를 구한다.
\(\overrightarrow{d}\) = (x - a, y - b)
(2) 센터 점 (a, b) 에서 반시계 방향으로 90도 회전하여 얻을 수 있는 점 (x', y') 으로의 방향 벡터를 \(\overrightarrow{d '}\) 이라고 할 때, 다음과 같은 식이 성립한다.

(3) \(\overrightarrow{d '}\) 와 센터 점 (a, b)를 이용하여 회전한 점 (x', y') 를 구할 수 있다.
(x', y') = \(\overrightarrow{d '}\) + (a, b)
위와 같은 방법으로 (g - 1) 세대 드래곤 커브의 정점들 중에 끝 점을 제외한 나머지 점들을 90도 회전하여 g 세대 드래곤 커브를 형성해주기만 하면 끝이다.
3번 방법은 g 세대 드래곤 커브의 정점들을 가지고 bool 2차원 배열에 정점 마다 true 를 할당해주면 된다.
이때 bool Map[101][101] 을 전역변수로 설정한다.
4번 방법은 임의의 점 (x, y) 에 대해서 (x, y), (x, y + 1), (x + 1, y), (x + 1, y + 1) 네 개의 점들이 존재해야만 1x1 정사각형이 만들어진다.
네 개 전부 true 인 경우에 카운팅해주면 된다.
Solution Code
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <string>
#include <iostream>
#include <algorithm>
#include <vector>
#include <queue>
#include <map>
#define INF 1000000000
#define endl '\n'
using namespace std;
const int RIGHT = 0, UP = 1, LEFT = 2, DOWN = 3;
vector<pair<int, int>> v;
bool Map[101][101];
pair<int, int> get_direct_vector(pair<int, int> center, pair<int, int> cur) {
pair<int, int> ret;
ret.first = cur.first - center.first;
ret.second = cur.second - center.second;
return ret;
}
pair<int, int> rotate_90(pair<int, int> direct_vector) {
pair<int, int> ret;
ret.first = -direct_vector.second;
ret.second = direct_vector.first;
return ret;
}
pair<int, int> get_point(pair<int, int> center, pair<int, int> direct_vector) {
pair<int, int> ret;
ret.first = center.first + direct_vector.first;
ret.second = center.second + direct_vector.second;
return ret;
}
void make_generation(int x,int y, int d, int g) {
int v_size;
pair<int, int> center;
// 0세대 드래곤 커브를 형성
switch (d) {
case UP: v.push_back({ x, y - 1 }); break;
case DOWN: v.push_back({ x, y + 1 }); break;
case RIGHT: v.push_back({ x + 1, y }); break;
case LEFT: v.push_back({ x - 1, y });
}
// g세대 드래곤 커브를 형성
while (g) {
v_size = v.size();
center.first = v[v_size - 1].first, center.second = v[v_size - 1].second;
pair<int, int> direct_vector, new_point;
for (int i = v_size - 2; i >= 0; i--) {
direct_vector = get_direct_vector(center, v[i]);
direct_vector = rotate_90(direct_vector);
new_point = get_point(center, direct_vector);
v.push_back(new_point);
}
g--;
}
// g세대 드래곤 커브의 모든 점들을 100x100 격자 위에 표시
for (int i = 0; i < v.size(); i++) {
Map[v[i].first][v[i].second] = true;
}
}
void input() {
int x, y, d, g;
cin >> x >> y >> d >> g;
v.clear();
v.push_back({ x, y });
Map[x][y] = true;
make_generation(x, y, d, g);
}
int main() {
ios_base::sync_with_stdio(false); cin.tie(0); cout.tie(0);
int n, cnt;
cin >> n;
while (n--) input();
cnt = 0;
for (int i = 0; i <= 99; i++) {
for (int j = 0; j <= 99; j++) {
if (Map[i][j] && Map[i][j + 1] && Map[i + 1][j] && Map[i + 1][j + 1])
cnt++;
}
}
cout << cnt;
return 0;
}
'백준 > simulation' 카테고리의 다른 글
| [백준 19236] 청소년 상어 (0) | 2022.03.31 |
|---|---|
| [백준 15683] 감시 (0) | 2021.08.31 |
| [백준 14891] 톱니바퀴 (0) | 2021.08.30 |
| [백준 14890] 경사로 (0) | 2021.08.29 |
| [백준 14499] 주사위 굴리기 (0) | 2021.08.29 |



