mojo's Blog
Optimal vertex cover, Makespan 본문
Claim: S is not much larger than the optimal vertex cover Sopt .
S가 최적의 vertex cover Sopt 보다 더 크지 않다고 한다.
왜 그런지 알아보도록 한다.
Note first that |S| = 2k where k is the number of edges that our algorithm pebbled.
Since k edges have no vertices in common, and since each one has at least one endpoint in Sopt ,
we have |Sopt | ≥ k.
Thus, S is at most twice as large as Sopt ,

여기서 k는 앞에서 사용했던 알고리즘으로 조약돌을 놓은 간선의 수이며 따라서 |S| = 2k 이다.
k개의 모서리는 공통의 꼭짓점이 없기 때문에, 그리고 각각의 꼭짓점이 Sopt 에 적어도 하나의 끝점을 가지고
있기 때문에, |Sopt | ≥ k를 가진다.
따라서, S는 최대 Sopt 의 두 배이며 ρ 값은 최대 2 값을 갖게 된다는 것을 알 수 있다.
This upper bound on ρ is tight.

Can we do better?
The pebble games achieves ρ = 2 by putting pebbles on both endpoints of any unpebbled edge.
Let’s now put just one pebble on an unpebbled edge that will have the effect of covering
as many unpebbled edges as possible.
Define the degree of a vertex as the number of uncovered edges it is a part of.
Then each step of this greedy algorithm chooses a vertex v of maximal degree and covers it.
This type of algorithm derived from “rule-of-thumb” reasoning is called a heuristic.
이제 최대한 많이 다듬어지지 않은 간선을 커버할 수 있는 다듬어지지 않은 가장자리에 조약돌 하나를
올려 놓음으로써 최대한 커버한 정점들의 갯수를 minimize 하는 방법이 도입된다.
이러한 탐욕 알고리즘의 각 단계는 최대 degree를 가진 꼭지점 v를 선택하고 그것을 덮는 방법이다.
"rule-of-thumb" 추론에서 파생된 이러한 유형의 알고리즘은 heuristic이라고 불린다.
그렇다면 heuristic 알고리즘을 활용한 vertex cover 를 직접 해보도록 하자.
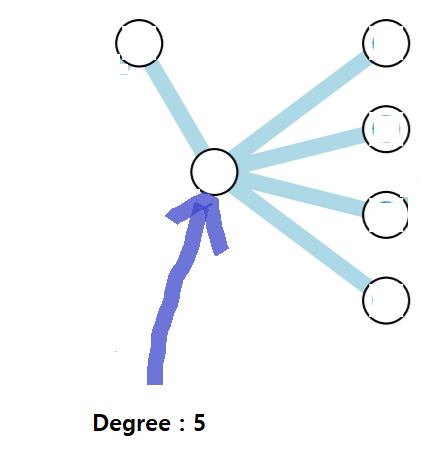

현재 그래프에서 가장 차수가 높은 것은 5이므로 해당 점에 조약돌을 놓도록 한다.
조약돌을 놓고 나서 더이상 조약돌을 놓을 수 없는 상태가 되버린다.
만약 해당 정점이 아닌 다른 곳에 조약돌을 놓을 경우, 5개의 조약돌을 놓게 되며 당연하게도
minimization 기법에 있어서 critical 하다는 것을 볼 수 있겠다.
While this greedy heuristic seems smarter than the pebble game, it is actually much worse.
It has ρ = Θ(log n)
이러한 greedy heuristic은 조약돌 게임보다 더 똑똑한 것처럼 보이지만, 사실은 훨씬 더 나쁘다고 한다.
이것의 값은 ρ = Θ(log n) 이라고 한다.
Consider the bipartite graph Bt = (W, U1 ∪ · · · Ut ) where W = {1, · · · , t} and Ui = {ui,1, · · · , ui,⌊t/i⌋}
for 1 ≤ i ≤ t.
bipartite graph Bt 에 대한 그래프를 일단 살펴보도록 하자.

t = 6 일 경우 W = {1, 2, ..., 6} 이고 Ui = {ui,1, · · · , ui,⌊t/i⌋} 에 대해서 i = 1, ..., 6 일 경우를 살펴보도록 한다.
i = 1) U1 = {u1,1, ..., u1,6}, U1에 총 6개의 vertex가 존재한다.
i = 2) U2 = {u2,1, ..., u2,3}, U2에 총 3개의 vertex가 존재한다.
i = 3) U3 = {u3,1, ..., u3,2}, U3에 총 2개의 vertex가 존재한다.
i = 4) U4 = {u4,1}, U4에 총 1개의 vertex가 존재한다.
i = 5) U5 = {u5,1}, U5에 총 1개의 vertex가 존재한다.
i = 6) U6 = {u6,1}, U6에 총 1개의 vertex가 존재한다.
The total number of vertices, n, is
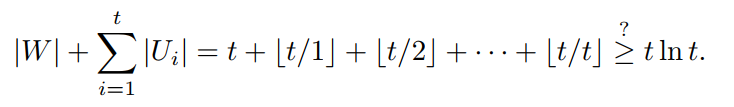
따라서 모든 정점들의 갯수는 위 식과 같이 세팅된다.
W에 속한 모든 정점들의 갯수와 U1, ..., Ut 에 속한 모든 정점들의 갯수를 더하면 위와 같다.
tlnt 에 대한 경우는 어떻게 나왔는지 아래 식에서 확인해보도록 하자.

먼저 ⌊t/i⌋ ≥ (t/i - 1) 라는 성질을 이용한 것으로 확인할 수 있겠다.
그리고 Harmonic number Ht 를 이용함으로써 Ht 가 lnt 이상인 성질을 통해 tlnt 가 최종적으로 나온것을 알 수 있다.
Connect uij to wk if ⌈k/i⌉ = j.
So each vertex in Ui has degree i.
Since each vertex in W is connected to at most one vertex in Ui for each i,
it has degree at most t.

예를 들어서 U4 일 경우 u41 -> w1, w2, w3, w4 만 허용된다.
만약 k = 5 일 경우 ⌈5/4⌉ = 2, 즉 1을 넘어버리는데 u42 에 대한 정점은 존재하지 않는다.
따라서 위와 같이 연결이 하게 된다면 Ui에 속한 각 정점의 degree는 자연스럽게 i가 되고,
W에 속한 각 정점의 차수는 최대 t가 되는 것을 알 수 있다.
The single vertex in Ut is the vertex of maximum degree t.
If we cover it, the degree of each vertex in W decreases by one, and the vertex in Ut−1 now
has maximum degree t − 1.
Covering this vertex leaves us with Ut−2 and so on.

위 사진은 윗 설명으로 U6 의 하나의 정점을 cover 한 모습이다.
이 방법은 greedy heuristic 을 이용한 기법으로 가장 차수가 높은 vertex 를 cover 하는 방식임을 알 수 있다.
Ut에 속한 하나의 vertex는 가장 높은 차수 t값을 보유하고 있다.
따라서 이 정점를 cover 할 경우 W에 속한 각 정점들의 차수가 1씩 감소하게 됨으로써
자연스럽게 Ut-1 에 속한 정점이 최대 차수 t - 1개를 보유하게 된다.
이를 반복해서 수행이 가능함을 짐작할 수 있겠다.
After we have covered all of Uj for all j > i, the vertices in Ui still have degree i and
the vertices in W have degree at most i.
모든 j > i에 대해 Uj를 모두 cover 한 후에도, Ui의 꼭짓점은 여전히 차수 i를 가지며 W의 꼭짓점은
최대 차수 i를 가지게 된다.
The greedy algorithm covers every vertex in U = U1 ∪ ... ∪ Ut and produces
a vertex cover S of size

결국 Ut 부터 차근차근 cover 함으로써 u1 까지 cover 를 하게 되므로 U1 부터 Ut 까지 모든 정점들의 갯수가
vertex cover S의 size가 되는 것을 짐작할 수 있다.
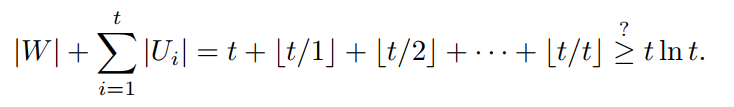
위 식을 이용하여 vertex cover S의 size |S| 를 구할 수 있게 된다.
But W is also a vertex cover and thus the size of the optimal one is

Fortunately (?), the greedy heuristic achieves ρ = O(log n) on any graph.
W에 속한 정점들을 전부 cover 해도 그 또한 vertex cover S가 된다.
따라서 위와 같이 최적화된 size는 t 이하가 될 수 있으며 ρ 값이 최소 O(log n) 임을 증명하였다.
Let’s look at another problem.
Suppose you run a parallel computer with p processors, p some constant, and are given
n jobs with running times t1, · · · , tn.
Goal is to find a schedule f : {1, · · · , n} → {1, · · · p} that assigns the jth job to the
f(j)th machine to minimize a value to be defined.
병렬 컴퓨터를 p 프로세서, p 상수, 그리고 실행 시간 t1, · · ·, tn으로 n개의 작업이 주어진다고 가정한다.
목표는 정의될 값을 최소화하기 위해 j번째 작업을 f(j)번째 기계에 할당하는 스케줄
f : {1, · · , n} → {1, · · p}를 정의하는 것이다.
The load on the jth machine is the total time it takes to run the jobs assigned to it,
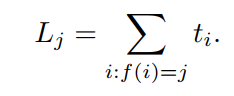
So the time it takes to finish all the jobs is the maximum load on any machine,

This time is called the makespan, and our goal is to minimize it.

위 그림으로 모든게 설명이 되었다.
Lj 같은 경우는 i = 1, ..., n 에 대한 job 중에 f(i) 의 값이 j 인 경우 시행 되어지는 모든 ti 의 값의 합으로 표현한다.
즉, L3 = t1 + t4 + t9 + t13 이면서 f(1) = f(4) = f(9) = f(13) = 3 임을 짐작할 수 있겠다.
그리고 이러한 Lj 들 중에 최댓값을 M 이라고 할 때, 이를 makespan 이라고 부르며 우리의 목표는
이를 minization 하는 것이다.
makespan
Input: A set of n running times ti ≥ 0, i = 1, · · · , n
Output: A function f : {1, · · · , n} → {1, · · · , p} that minimizes the makespan M

It can be shown that makespan is NP-hard.
However, there is an approximation algorithm that comes to a quality guarantee.
Let Ttot = t1 + ... + tn be the total running time of all tasks.
Divide tasks into “large” and “small” groups where we call the jth task large if its running time
tj ≥ η * Ttot for some η, say, 1/10, and small otherwise.
작업을 "큰" 그룹과 "작은" 그룹으로 나눕니다.
여기서 j번째 작업은 실행 시간 tj ≥ ηTtot이면 큰 작업이라고 부르고, 그렇지 않으면 작은 작업이라고 합니다.
Algorithm proceeds in two phases:
1. Find a schedule that minimizes the makespan of the large tasks using exhaustive search.
2. Distribute the small tasks by giving each one to the machine with the smallest load so far.
두 단계를 통한 알고리즘 진행방법은 다음과 같다.
(1) 철저한 검색을 통해 대형 작업의 소요 시간을 최소화하는 일정을 찾고,
(2) 지금까지의 부하가 가장 적은 기계에 각각 주어 작은 작업을 분배한다.
Since there are at most 1/η large tasks, there are p^(1/η) ways, or a constant number
of ways to schedule them.
Phase 2 clearly runs in polynomial time also.
큰 작업은 많아야 1/η개이므로 p^(1/η) 방법 또는 일정 수의 스케줄 지정 방법이 있다.
2단계는 polynomial time 으로 실행된다.
How does M compare to Mopt ?
Let Mlarge = minimum makespan of the large tasks. (Mlarge ≤ Mopt .)
If the algorithm fits all the small tasks in phase 2 without increasing the makespan,
then M = Mlarge .
Since Mopt ≤ M , we have M = Mopt in this case.
Suffices to consider only the case where makespan increases in phase 2 and where our schedule
for the small tasks might not be optimal.
Let Lj = the load of machine j after phase 2.
Wlog, assume that L1 ≥ L2 ≥ · · · ≥ Lp .
Since L1 = M > Mlarge, we know at least one small task was added to machine 1.
Let t = running time of the last such task.
2단계 후, Lj = 기계 j의 load가 발생하도록 한다.
그리고 Wlog으로 L1 ≥ L2 ≥ · · · ≥ Lp 라고 가정한다.
L1 = M > M large 이므로, 기계 1에 적어도 하나의 작은 작업이 추가되었음을 알고 있다.
이러한 마지막 작업의 실행 시간을 t 로 설정한다.
Since our algorithm greedily assigns small tasks to the machines with the smallest load,
the load of machine 1 must have been ≤ others just before this task was added.

가장 작은 load 를 가진 기계에 작은 작업을 탐욕스럽게 할당하기 때문에,
기계 1의 load는 이 작업이 추가되기 바로 전에 다른 load들 보다 작거나 같아야 한다.
즉, 위와 같은 부등식이 성립한다.
Since t < ηTtot ,

On the other hand, the best schedule would keep all the machines busy all the time.
⇒ Mopt ≥ Ttot/p
Combining the above two gives the following:

By setting η = ǫ/(p − 1), we can approximate Mopt within a factor of 1 + ǫ for arbitrarily
small ǫ > 0.
For each fixed ǫ, this algorithm runs in polynomial time, and is called a
polynomial-time approximation scheme or PTAS.
Note, however, running time increases as ǫ decreases.
In phase 1, p^(1/η) = p^(p - 1/ǫ) possible schedules need to be explored,
so running time grows exponentially as a function of 1/ǫ.
An algorithm whose running time is polynomial both in n and 1/ǫ is called a fully
polynomial-time approximation scheme or FPTAS.
η = ǫ/(p - 1)을 설정하여 임의의 작은 ǫ > 0에 대해 1 + ǫ의 계수 내에서 Mopt를 근사할 수 있다.
각 고정된 ǫ에 대해서, 이 알고리즘은 다항식 시간으로 실행되며, 다항식 시간 근사 체계 또는 PTAS라고 불린다.
그러나 ǫ가 감소하면 실행 시간이 증가한다.
1단계에서는 p^(1/η) = p^(p - 1/ǫ) 와 같은 가능한 일정을 탐색할 필요가 있으므로 실행 시간
1/ǫ 의 함수로 기하급수적으로 증가한다.
실행 시간이 n과 1/ǫ 모두에서 다항식인 알고리즘을 완전 다항식 시간 근사 체계 또는 FPTAS라고 한다.
'학교에서 들은거 정리 > 자동장치' 카테고리의 다른 글
| traveling salesman, min set cover (0) | 2021.12.18 |
|---|---|
| Optimization and Approximation (0) | 2021.12.07 |
| Maximizing and Minimizing (0) | 2021.12.02 |
| balanced k-coloring (0) | 2021.11.30 |
| Designing Reduction (0) | 2021.11.25 |




