mojo's Blog
[백준 23743] 방탈출 본문
문제 링크 => 23743번: 방탈출 (acmicpc.net)
23743번: 방탈출
첫 번째 줄에는 방의 개수 $N$과 설치할 수 있는 워프의 개수 $M$이 주어진다. ($2 \le N \le 200\,000$, $1 \le M \le 100\,000$) 다음 $M$개의 줄에는 워프의 정보를 나타내는 세 정수 $a_i$, $b_i$, $c_i$가 공백으
www.acmicpc.net
방탈출 카페에는 1번부터 N번까지 총 N개의 방이 있고, 각 방에는 친구들이 한 명씩 들어가 있다.
모든 방은 외부로부터 완전히 독립되어 있다.
방에서 탈출하지 못하는 친구들이 답답했던 원빈이는 모든 친구들이 출구로 탈출할 수 있도록 워프와
비상탈출구를 설치하려고 한다.
워프는 최대 M개까지 설치할 수 있는데, i번째 워프는 설치하는 데 ci의 시간이 걸리고, 워프를 설치하면
ai번 방과 bi번 방 사이를 이동할 수 있다.
또한 각 방에는 출구로 바로 연결되는 비상탈출구를 설치할 수 있는데, i번 방에 비상탈출구를 설치하는 데
걸리는 시간은 ti이다.
모든 친구들이 출구로 탈출할 수 있도록 워프와 비상탈출구를 설치하는 데 걸리는 최소 시간을 구해보자.
최소 스패닝 트리 문제이다.
이 문제를 보면서 다음과 같은 그림이 떠올랐다.
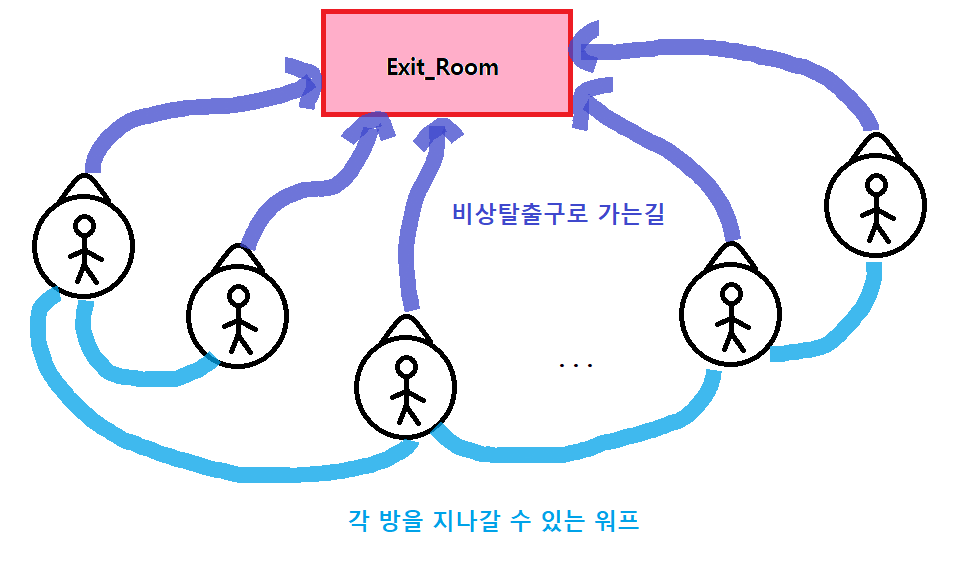
비상탈출구로 갈 수 있는 더미 노드 하나를 추가하여 Kruskal's Algorithm을 활용하여 얻을 수 있는 MST에 대해서
총 거리를 구해야 겠다는 생각을 하였다.
각 방의 노드 번호를 i 라고 할 때(i = 1, ..., N) 비상탈출구에 대한 노드 번호를 N + 1 로 부여하였고 input 으로 주어진
간선들에 대해서 연결하여 해결하였다.
Solution Code
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdlib.h>
struct Edge {
int src, dest, weight;
};
struct Graph {
int V, E;
struct Edge* edge;
};
struct Graph* createGraph(int V, int E){
struct Graph* graph = (struct Graph*)malloc(sizeof(struct Graph));
graph->V = V;
graph->E = E;
graph->edge = (struct Edge*)malloc(graph->E * sizeof(struct Edge));
return graph;
}
struct subset {
int parent;
int rank;
};
int find(struct subset subsets[], int i) {
if (subsets[i].parent != i)
subsets[i].parent = find(subsets, subsets[i].parent);
return subsets[i].parent;
}
void Union(struct subset subsets[], int x, int y) {
int xroot = find(subsets, x);
int yroot = find(subsets, y);
if (subsets[xroot].rank < subsets[yroot].rank)
subsets[xroot].parent = yroot;
else if (subsets[xroot].rank > subsets[yroot].rank)
subsets[yroot].parent = xroot;
else {
subsets[yroot].parent = xroot;
subsets[xroot].rank++;
}
}
int myComp(const void* a, const void* b) {
struct Edge* a1 = (struct Edge*) a;
struct Edge* b1 = (struct Edge*)b;
return a1->weight - b1->weight;
}
int KruskalMST(struct Graph* graph) {
int V = graph->V;
int e, i, total;
e = i = total = 0;
qsort(graph->edge, graph->E, sizeof(struct Edge), myComp);
struct subset* subsets = (struct subset*)malloc((V + 2) * sizeof(struct subset));
for (int v = 1; v <= V + 1; v++) {
subsets[v].parent = v;
subsets[v].rank = 0;
}
while (e < V - 1) {
struct Edge next_edge = graph->edge[i++];
int x = find(subsets, next_edge.src);
int y = find(subsets, next_edge.dest);
if (x != y) {
e++;
total += next_edge.weight;
Union(subsets, x, y);
}
}
return total;
}
int main()
{
int V, E, a, b, dist;
scanf("%d %d", &V, &E);
struct Graph* graph = createGraph(V + 1, V + E);
// 워프 처리
for (int i = 0; i < E; i++) {
scanf("%d %d %d", &a, &b, &dist);
graph->edge[i].src = a;
graph->edge[i].dest = b;
graph->edge[i].weight = dist;
}
// 비상 출구 처리
for (int i = 0; i < V; i++) {
scanf("%d", &dist);
graph->edge[E + i].src = i + 1;
graph->edge[E + i].dest = V + 1;
graph->edge[E + i].weight = dist;
}
printf("%d", KruskalMST(graph));
return 0;
}
'백준 > Graph' 카테고리의 다른 글
| [백준 11404] 플로이드 (0) | 2021.12.06 |
|---|---|
| [백준 11779] 최소비용 구하기 2 (0) | 2021.12.01 |
| [백준 11378] 열혈강호 4 (2) | 2021.11.10 |
| [백준 2056] 작업 (0) | 2021.11.08 |
| [백준 6087] 레이저 통신 (0) | 2021.11.06 |




